题目内容
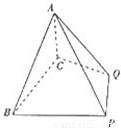
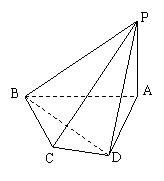
如图:四棱锥A-BCQP中,二面角A-BC-P为90°,且∠BAC=∠BCQ=90°,∠CBP=45°BP+AP=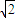 BC,AB=AC=
BC,AB=AC=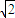 B.
B.(Ⅰ)求证:平面AB⊥平面ACQ;
(Ⅱ)求直线AP与平面ACQ所成角的大小.
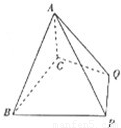
【答案】分析:(Ⅰ)证明AB⊥AC,AB⊥QC,利用线面垂直的判定可得AB⊥平面ACQ;
(Ⅱ)设线段BC的中点是O,连接OP,OA,设PO′⊥平面ACQ于O′,则∠PAO′是AP与平面ACQ所成的角,∠PAO′与∠BAP互余,求得∠BAP=60°,即可得到结论.
解答: (Ⅰ)证明:∵∠BAC=90°,∴AB⊥AC
(Ⅰ)证明:∵∠BAC=90°,∴AB⊥AC
∵侧面ABC⊥底面BCQP且∠BCQ=90°,∴QC⊥平面ABC
∵AB?平面ABC
∴AB⊥QC
∵AC∩QC=C
∴AB⊥平面ACQ;
(Ⅱ)解:设线段BC的中点是O,连接OP,OA
设PO′⊥平面ACQ于O′,则∠PAO′是AP与平面ACQ所成的角
由(Ⅰ)知AB⊥平面ACQ,AB∥PO′,∠PAO′与∠BAP互余
∵AB=AC=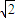 ,∠BAC=90°,∴BC=2,AO⊥BC,∴AO⊥平面BCQP
,∠BAC=90°,∴BC=2,AO⊥BC,∴AO⊥平面BCQP
设BP=x,∵BP+AP=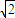 BC,∴AP=2
BC,∴AP=2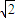 -x,AO=BO=1,OP2=(2
-x,AO=BO=1,OP2=(2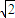 -x)2-1
-x)2-1
在△OPB中,由余弦定理得OP2=OB2+BP2-2OB×BPcos45°,∴x=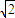
∴△ABP为等边三角形
∴∠BAP=60°
∴∠PAO′=30°,即直线AP与平面ACQ所成角为30°.
点评:本题考查线面垂直,考查线面角,解题的关键是掌握线面垂直的判定,正确作出线面角,属于中档题.
(Ⅱ)设线段BC的中点是O,连接OP,OA,设PO′⊥平面ACQ于O′,则∠PAO′是AP与平面ACQ所成的角,∠PAO′与∠BAP互余,求得∠BAP=60°,即可得到结论.
解答:
 (Ⅰ)证明:∵∠BAC=90°,∴AB⊥AC
(Ⅰ)证明:∵∠BAC=90°,∴AB⊥AC∵侧面ABC⊥底面BCQP且∠BCQ=90°,∴QC⊥平面ABC
∵AB?平面ABC
∴AB⊥QC
∵AC∩QC=C
∴AB⊥平面ACQ;
(Ⅱ)解:设线段BC的中点是O,连接OP,OA
设PO′⊥平面ACQ于O′,则∠PAO′是AP与平面ACQ所成的角
由(Ⅰ)知AB⊥平面ACQ,AB∥PO′,∠PAO′与∠BAP互余
∵AB=AC=
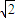 ,∠BAC=90°,∴BC=2,AO⊥BC,∴AO⊥平面BCQP
,∠BAC=90°,∴BC=2,AO⊥BC,∴AO⊥平面BCQP设BP=x,∵BP+AP=
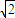 BC,∴AP=2
BC,∴AP=2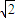 -x,AO=BO=1,OP2=(2
-x,AO=BO=1,OP2=(2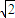 -x)2-1
-x)2-1在△OPB中,由余弦定理得OP2=OB2+BP2-2OB×BPcos45°,∴x=
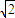
∴△ABP为等边三角形
∴∠BAP=60°
∴∠PAO′=30°,即直线AP与平面ACQ所成角为30°.
点评:本题考查线面垂直,考查线面角,解题的关键是掌握线面垂直的判定,正确作出线面角,属于中档题.

练习册系列答案
相关题目
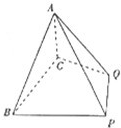 (2012•南宁模拟)如图:四棱锥A-BCQP中,二面角A-BC-P为90°,且∠BAC=∠BCQ=90°,∠CBP=45°BP+AP=
(2012•南宁模拟)如图:四棱锥A-BCQP中,二面角A-BC-P为90°,且∠BAC=∠BCQ=90°,∠CBP=45°BP+AP=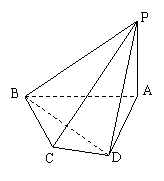
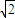 BC,AB=AC=
BC,AB=AC=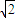 B.
B.