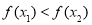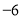题目内容
 两城相距
两城相距 ,在两地之间距
,在两地之间距 城
城 处
处 地建一核电站给
地建一核电站给 两城供电.为保证城市安全,核电站距城市距离不得少于
两城供电.为保证城市安全,核电站距城市距离不得少于 .已知供电费用(元)与供电距离(
.已知供电费用(元)与供电距离( )的平方和供电量(亿度)之积成正比,比例系数
)的平方和供电量(亿度)之积成正比,比例系数 ,若
,若 城供电量为
城供电量为 亿度/月,
亿度/月, 城为
城为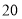 亿度/月.
亿度/月.
(Ⅰ)把月供电总费用 表示成
表示成 的函数,并求定义域;
的函数,并求定义域;
(Ⅱ)核电站建在距 城多远,才能使供电费用最小,最小费用是多少?
城多远,才能使供电费用最小,最小费用是多少?
(Ⅰ) ,定义域为
,定义域为 ;(Ⅱ)核电站建在距
;(Ⅱ)核电站建在距 城
城 时,才能使供电费用最小,最小费用为
时,才能使供电费用最小,最小费用为 元.
元.
【解析】
试题分析:(Ⅰ)利用供电费用=电价×电量可建立函数,同时根据题设要求写出其定义域;(Ⅱ)根据﹙Ⅰ﹚所得函数的解析式及定义域,通过配方,根据二次函数的性质可求得最值,进而确定电站所建的位置.
试题解析:(Ⅰ) ,即
,即 ,
,
由 得
得 ,
,
所以函数解析式为  ,定义域为
,定义域为 .
.
(Ⅱ)由 得
得 ,
,
因为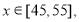 所以
所以 在
在 上单调递增,所以当
上单调递增,所以当 时,
时, .
.
故当核电站建在距 城
城 时,才能使供电费用最小,最小费用为
时,才能使供电费用最小,最小费用为 元.
元.
考点:函数的实际应用.

练习册系列答案
相关题目
某种计算机病毒是通过电子邮件进行传播的,下表是某公司前5天监测到的数据:
第 | 1 | 2 | 3 | 4 | 5 |
被感染的计算机数量 | 10 | 20 | 39 | 81 | 160 |
则下列函数模型中能较好地反映计算机在第 天被感染的数量
天被感染的数量 与
与 之间的关系的是 ( )
之间的关系的是 ( )
A. B.
B. C.
C. D.
D.