题目内容
已知F1、F2是双曲线C:x2-
=1的两个焦点,若离心率等于
的椭圆E与双曲线C的焦点相同.
(1)求椭圆E的方程;
(2)如果动点P(m,n)满足|PF1|+|PF2|=10,曲线M的方程为:
+
=1.判断直线l:mx+ny=1与曲线M的公共点的个数,并说明理由;当直线l与曲线M相交时,求直线l:mx+ny=1截曲线M所得弦长的最大值.
| y2 |
| 15 |
| 4 |
| 5 |
(1)求椭圆E的方程;
(2)如果动点P(m,n)满足|PF1|+|PF2|=10,曲线M的方程为:
| x2 |
| 2 |
| y2 |
| 2 |
分析:(1)由双曲线的方程即可得出焦点坐标,即可得出椭圆的焦点坐标公式,利用椭圆的标准方程及其性质即可得出方程;
(2)由动点P(m,n)满足|PF1|+|PF2|=10,可知点P在椭圆E上,即可得出m与n的关系及其取值范围.因为曲线M是圆心为(0,0),半径为r=
的圆,利用点到直线的距离公式可得:圆心(0,0)到直线l:mx+ny-1=0的距离,即可得出直线l:mx+ny=1与曲线M公共点的个数.设直线l:mx+ny=1截曲线M所得弦长t,t=2
=2
利用在0≤m2≤25上单调性,即可得出t的最大值.
(2)由动点P(m,n)满足|PF1|+|PF2|=10,可知点P在椭圆E上,即可得出m与n的关系及其取值范围.因为曲线M是圆心为(0,0),半径为r=
| 2 |
| r2-d2 |
2-
|
解答:解:(1)∵F1、F2是双曲线C:x2-
=1的两个焦点,∴c=
=4
不妨设F1(-4,0)、F2(4,0).
∵椭圆E与双曲线C的焦点相同.
∴设椭圆E的方程为
+
=1(a>b>0)
∵根据已知得
,解得
∴椭圆E的方程为
+
=1
(2)直线l:mx+ny=1与曲线M有两个公共点.
理由是:
∵动点P(m,n)满足|PF1|+|PF2|=10,∴P(m,n)是椭圆E上的点,
∴
+
=1,∴n2=9-
m2,0≤m2≤25
∵曲线M是圆心为(0,0),半径为r=
的圆
圆心(0,0)到直线l:mx+ny-1=0的距离d=
=
≤
=
<
∴直线l:mx+ny=1与曲线M有两个公共点.
设直线l:mx+ny=1截曲线M所得弦长t,t=2
=2
在0≤m2≤25上递增
∴当m2=25,m=±5,n=0,即l:x=±
时,t最大为
.
| y2 |
| 15 |
| 1+15 |
不妨设F1(-4,0)、F2(4,0).
∵椭圆E与双曲线C的焦点相同.
∴设椭圆E的方程为
| x2 |
| a2 |
| y2 |
| b2 |
∵根据已知得
|
|
∴椭圆E的方程为
| x2 |
| 25 |
| y2 |
| 9 |
(2)直线l:mx+ny=1与曲线M有两个公共点.
理由是:
∵动点P(m,n)满足|PF1|+|PF2|=10,∴P(m,n)是椭圆E上的点,
∴
| m2 |
| 25 |
| n2 |
| 9 |
| 9 |
| 25 |
∵曲线M是圆心为(0,0),半径为r=
| 2 |
圆心(0,0)到直线l:mx+ny-1=0的距离d=
| 1 | ||
|
| 1 | ||||
|
| 1 | ||
|
| 1 |
| 3 |
| 2 |
∴直线l:mx+ny=1与曲线M有两个公共点.
设直线l:mx+ny=1截曲线M所得弦长t,t=2
| r2-d2 |
2-
|
∴当m2=25,m=±5,n=0,即l:x=±
| 1 |
| 5 |
| 14 |
| 5 |
点评:熟练掌握圆锥曲线的定义及其性质、直线与圆锥曲线的位置关系、点到直线的距离公式、弦长公式、函数的单调性等是解题的关键.

练习册系列答案
相关题目
已知F1,F2分别为双曲
-
=1(a>0,b>0)的左、右焦点,P为双曲线左支上任一点,若
的最小值为8a,则双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、(1,+∞) |
| B、(0,3] |
| C、(1,3] |
| D、(0,2] |
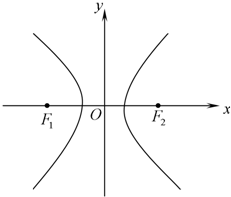
 的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.
的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.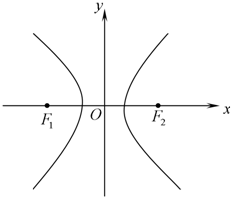
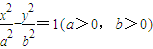 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若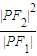 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )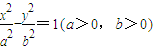 的左、右焦点,P为双曲线左支上任一点,若
的左、右焦点,P为双曲线左支上任一点,若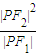 的最小值为8a,则双曲线的离心率e的取值范围是( )
的最小值为8a,则双曲线的离心率e的取值范围是( )