题目内容
设a>0且a≠1,若P=loga(a3+1),Q=loga(a2+1),试比较P、Q的大小.
答案:
解析:
提示:
解析:
①当0<a<1时,由y=ax在(-∞,+∞)上递减知a3<a2,即a3+1<a2+1又当0<a<1时,y=logax在(0,+∞)上递减 ∴loga(a3+1)>loga(a2+1)即P>Q ②当a>1时,有a3>a2即a3+1>a2+1∴loga(a3+1)>loga(a2+1)即P>Q. 总之有P>Q |
提示:
本题是利用对数函数和指数函数的单调性比较函数值的大小,要注意掌握数学中分类讨论的思想方法. |

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
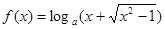 (x≥1)
(x≥1)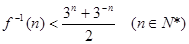 ,求a的取值范围。
,求a的取值范围。 (a>0且a≠1) ,则当f (x)为可等射函数时,a的取值范围是
(a>0且a≠1) ,则当f (x)为可等射函数时,a的取值范围是