题目内容
设平面三点A(1,0),B(0,1),C(2,5).
(Ⅰ)试求向量2
+
的模
(Ⅱ)试求向量
与
的夹角;
(Ⅲ)试求与
垂直的单位向量的坐标.
(Ⅰ)试求向量2
| AB |
| AC |
(Ⅱ)试求向量
| AB |
| AC |
(Ⅲ)试求与
| BC |
分析:(Ⅰ)由题意先求出
,
,然后代入求解2
+
,即可求解
(Ⅱ)先求|
|,|
|=
,然后求出
•
,代入向量的夹角公式cosA=
即可求解
(Ⅲ)设所求向量为
=(x,y),则x2+y2=1. 然后由由
⊥
,利用向量的数量积的性质可得关于x,y的方程,联立可求x,y即可求解
| AB |
| AC |
| AB |
| AC |
(Ⅱ)先求|
| AB |
| AC |
| 12+52 |
| AB |
| AC |
| ||||
|
|
(Ⅲ)设所求向量为
| m |
| BC |
| m |
解答:解:(Ⅰ)∵
=(0-1,1-0)=(-1,1),
=(2-1,5-0)=(1,5).
∴2
+
=2(-1,1)+(1,5)=(-1,7).
∴|2
+
|=
=
=5
.…(4分)
(Ⅱ)∵|
|=
=
.
|
|=
=
,
•
=(-1)×1+1×5=4.
∴cosA=
=
=
.…(8分)
(Ⅲ)设所求向量为
=(x,y),则x2+y2=1. ①
又
=(2-0,5-1)=(2,4),由
⊥
,得2 x+4 y=0. ②
由①、②,得
或
∴
=(
,-
)或(-
,
).…(12分)
| AB |
| AC |
∴2
| AB |
| AC |
∴|2
| AB |
| AC |
| (-1)2+72 |
| 50 |
| 2 |
(Ⅱ)∵|
| AB |
| (-1)2+12 |
| 2 |
|
| AC |
| 12+52 |
| 26 |
| AB |
| AC |
∴cosA=
| ||||
|
|
| 4 | ||||
|
2
| ||
| 13 |
(Ⅲ)设所求向量为
| m |
又
| BC |
| BC |
| m |
由①、②,得
|
|
∴
| m |
2
| ||
| 5 |
| ||
| 5 |
2
| ||
| 5 |
| ||
| 5 |
点评:本题主要考查了向量的数量积的坐标表示的基本运算,向量数量积的运算性质的简单应用,属于基础试题

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 的值;
的值; 与
与 的夹角的余弦值;
的夹角的余弦值; 垂直的单位向量的坐标.
垂直的单位向量的坐标. 的值;
的值; 与
与 的夹角的余弦值;
的夹角的余弦值; 垂直的单位向量的坐标.
垂直的单位向量的坐标. +
+ 的模;
(2)若向量
的模;
(2)若向量 ,求
,求 。
。 +
+ 的模
的模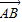 与
与 的夹角;
的夹角; 垂直的单位向量的坐标.
垂直的单位向量的坐标.