题目内容
设平面三点A(1,0),B(0,1),C(2,5).
(1)求 的值;
的值;
(2)求向量 与
与 的夹角的余弦值;
的夹角的余弦值;
(3)试求与 垂直的单位向量的坐标.
垂直的单位向量的坐标.
【答案】
(1) =4;(2)cos
=4;(2)cos  =
= .
.
(3)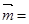 (
( ,-
,- )或
)或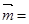 (-
(- ,
, ).
).
【解析】
试题分析:(1)∵  =(-1,1),
=(-1,1), =(1,5).
=(1,5).
∴  =(-1,1)
=(-1,1) (1,5)=4
(1,5)=4
(2)∵ | |=
|= =
= .|
.|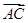 |=
|= =
= ,
,
 ·
· =4.∴ cos
=4.∴ cos  ? =
? = =
= =
= .
.
(3)设所求向量为 =(x,y),则
=(x,y),则 . ①
. ①
又  =(2,4),由
=(2,4),由

 ,得2 x +4 y =0. ②
,得2 x +4 y =0. ②
由①、②,得 或
或  ∴
∴ 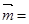 (
( ,-
,- )或
)或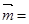 (-
(- ,
, ).
).
考点:本题主要考查平面向量的坐标运算,向量垂直的条件,向量的数量积。
点评:典型题,思路明确,需要逐步进行坐标运算,根据数量积的定义及夹角公式,达到解题目的。为求向量的坐标,根据向量垂直的条件,建立方程组求解。

练习册系列答案
相关题目
 的值;
的值; 与
与 的夹角的余弦值;
的夹角的余弦值; 垂直的单位向量的坐标.
垂直的单位向量的坐标. +
+ 的模;
(2)若向量
的模;
(2)若向量 ,求
,求 。
。 +
+ 的模
的模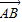 与
与 的夹角;
的夹角; 垂直的单位向量的坐标.
垂直的单位向量的坐标.