题目内容
 已知函数f(x)=Asin(ωx+φ)(其中x∈R,A>0,ω>0,
已知函数f(x)=Asin(ωx+φ)(其中x∈R,A>0,ω>0, <φ
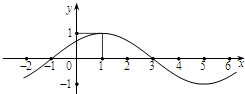
<φ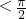 )的部分图象如图所示.
)的部分图象如图所示.
(Ⅰ)求函数f(x)的解析式及f(x)的单调递增区间;
(Ⅱ)已知在函数f(X)的图象上的三点M,N,P的横坐标分别为-1,1,5,求sin∠MNP的值.
解:(Ⅰ)由图可知,A=1,最小正周期T=4×2=8.
由T= =8,得ω=
=8,得ω= .…(3分)
.…(3分)
又f(1)=sin( +φ)=1,且
+φ)=1,且 <φ<
<φ< ,
,
所以φ= .…(5分)
.…(5分)
所以f(x)=sin( x+
x+ ).…(6分)
).…(6分)
由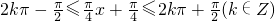 得8k-3≤x≤8k+1(k∈Z)
得8k-3≤x≤8k+1(k∈Z)
∴f(x)的单调递增区间为[8k-3,8k+1](k∈Z)…(8分)
(Ⅱ)因为f(-1)=0,f(1)=1,f(5)=-1,所以M(-1,0)N(1,1),P(5,-1).…(9分)
所以|MN|= ,|PN|=
,|PN|= ,|MP|=
,|MP|=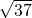 .
.
由余弦定理得cos∠MNP=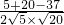 =-
=- .…(12分)
.…(12分)
因为∠MNP∈[0,π),所以sin∠MNP= .…(14分)
.…(14分)
分析:(Ⅰ)利用最值求得A,根据周期可求ω,结合最值点,可求φ,从而可得函数解析式,进而可得f(x)的单调递增区间;
(Ⅱ)利用函数解析式点M,N,P的坐标,结合余弦定理,即可求sin∠MNP的值.
点评:本题考查三角函数解析式的确定,考查函数的单调性,考查余弦定理的运用,属于中档题.
由T=
 =8,得ω=
=8,得ω= .…(3分)
.…(3分)又f(1)=sin(
 +φ)=1,且
+φ)=1,且 <φ<
<φ< ,
,所以φ=
 .…(5分)
.…(5分)所以f(x)=sin(
 x+
x+ ).…(6分)
).…(6分)由
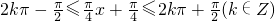 得8k-3≤x≤8k+1(k∈Z)
得8k-3≤x≤8k+1(k∈Z)∴f(x)的单调递增区间为[8k-3,8k+1](k∈Z)…(8分)
(Ⅱ)因为f(-1)=0,f(1)=1,f(5)=-1,所以M(-1,0)N(1,1),P(5,-1).…(9分)
所以|MN|=
 ,|PN|=
,|PN|= ,|MP|=
,|MP|=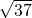 .
.由余弦定理得cos∠MNP=
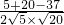 =-
=- .…(12分)
.…(12分)因为∠MNP∈[0,π),所以sin∠MNP=
 .…(14分)
.…(14分)分析:(Ⅰ)利用最值求得A,根据周期可求ω,结合最值点,可求φ,从而可得函数解析式,进而可得f(x)的单调递增区间;
(Ⅱ)利用函数解析式点M,N,P的坐标,结合余弦定理,即可求sin∠MNP的值.
点评:本题考查三角函数解析式的确定,考查函数的单调性,考查余弦定理的运用,属于中档题.

练习册系列答案
相关题目