题目内容
（2007•温州一模）已知两条不同直线a、b，两个平面α，β，且α∥β，a⊥α，设命题p：b∥β；命题q：a⊥b，则p是q成立的（ ）
分析：根据线面垂直的判定，可知a⊥β，由于b∥β，故a⊥b，反之，若a⊥b，则b∥β 或b?β，故可得结论．
解答：解：∵α∥β，a⊥α，∴a⊥β
∵b∥β，∴a⊥b
反之，若a⊥b，则b∥β 或b?β
故选A．
∵b∥β，∴a⊥b
反之，若a⊥b，则b∥β 或b?β
故选A．
点评：本题考查空间两条直线的位置关系，平面平行、垂直的判定及性质定理，解题时要综合考虑判定定理与性质定理的条件与结论．
练习册系列答案
相关题目
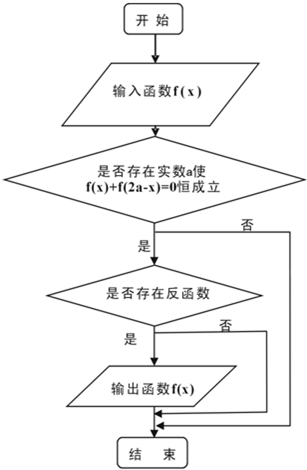（2007•温州一模）某流程如图所示，现输入如下四个函数，则可以输出的函数是（ ）