题目内容
(2007•温州一模)某高校在进行自主招生面试时,共设3道试题,每道试题回答正确给10分、否则都不给分.
(Ⅰ)某学生参加面试得分为20分的情况有几种?
(Ⅱ)若某学生对各道试题回答正确的概率均为
,求他至少得10分的概率.
(Ⅰ)某学生参加面试得分为20分的情况有几种?
(Ⅱ)若某学生对各道试题回答正确的概率均为
| 2 | 3 |
分析:(Ⅰ)由题意可得,此学生答对了3道题中的2道,故有C32种不同的情况.
(Ⅱ)他至少得10分的对立事件为:他得了零分,即他把3个题全部做错了,故对立事件的概率为(
)3,用1减去它的对立事件概率即为所求.
(Ⅱ)他至少得10分的对立事件为:他得了零分,即他把3个题全部做错了,故对立事件的概率为(
| 1 |
| 3 |
解答:解:(Ⅰ)某学生参加面试得分为20,说明此学生答对了3道题中的2道,故不同情况有C32=3种 ….(6分)
(Ⅱ)设该学生的得分为ξ,则ξ=0,10,20,30 …(8分)
P(ξ≥10)=1-P(ξ=0)=1-(
)3=
. …..(12分)
所以他至少得(10分)的概率为
. …..(14分)
(Ⅱ)设该学生的得分为ξ,则ξ=0,10,20,30 …(8分)
P(ξ≥10)=1-P(ξ=0)=1-(
| 1 |
| 3 |
| 26 |
| 27 |
所以他至少得(10分)的概率为
| 26 |
| 27 |
点评:本题主要考查n次独立重复实验中恰好发生k次的概率,等可能事件的概率,所求的事件的概率等于用1减去它的对立事件概率.

练习册系列答案
相关题目
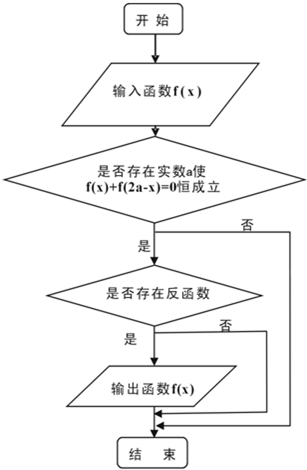 (2007•温州一模)某流程如图所示,现输入如下四个函数,则可以输出的函数是( )
(2007•温州一模)某流程如图所示,现输入如下四个函数,则可以输出的函数是( )