题目内容
(2007•温州一模)设等差数列{an}的前n项和为Sn,若a1=-5,且它的前11项的平均值是5.
(1)求等差数列的公差d;
(2)求使Sn>0成立的最小正整数n.
(1)求等差数列的公差d;
(2)求使Sn>0成立的最小正整数n.
分析:(1)由a1=-5,
=
=a6=5可求d
(2)由Sn=na1+
d=n2-6n>0可得n的范围,结合n为正整数可求
| a1+a2+…+a11 |
| 11 |
| 11a6 |
| 11 |
(2)由Sn=na1+
| n(n-1) |
| 2 |
解答:(本小题满分14分)
解:(1)∵a1=-5,
=
=a6=5
∴d=
=2.…(7分)
(2)∵Sn=na1+
d=n2-6n>0
∴n>6且n∈N*,∴使Sn>0成立的最小正整数n为7.…(14分)
解:(1)∵a1=-5,
| a1+a2+…+a11 |
| 11 |
| 11a6 |
| 11 |
∴d=
| a6-a1 |
| 6-1 |
(2)∵Sn=na1+
| n(n-1) |
| 2 |
∴n>6且n∈N*,∴使Sn>0成立的最小正整数n为7.…(14分)
点评:本题主要考查了等差数量的通项公式、等差数列的性质及求和公式的应用,属于基础性试题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
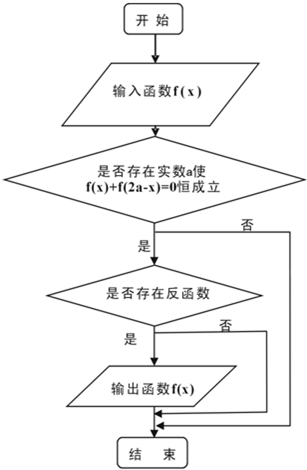 (2007•温州一模)某流程如图所示,现输入如下四个函数,则可以输出的函数是( )
(2007•温州一模)某流程如图所示,现输入如下四个函数,则可以输出的函数是( )