题目内容
已知以动点P为圆心的圆与直线y=-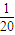 相切,且与圆x2+(y-
相切,且与圆x2+(y- )2=
)2=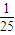 外切.
外切.(Ⅰ)求动P的轨迹C的方程;
(Ⅱ)若M(m,m1),N(n,n1)是C上不同两点,且 m2+n2=1,m+n≠0,直线L是线段MN的垂直平分线.
(1)求直线L斜率k的取值范围;
(2)设椭圆E的方程为
 +
+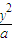 =1(0<a<2).已知直线L与抛物线C交于A、B两个不同点,L与椭圆E交于P、Q两个不同点,设AB中点为R,PQ中点为S,若
=1(0<a<2).已知直线L与抛物线C交于A、B两个不同点,L与椭圆E交于P、Q两个不同点,设AB中点为R,PQ中点为S,若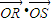 =0,求E离心率的范围.
=0,求E离心率的范围.
【答案】分析:(Ⅰ)根据动点P为圆心的圆与直线y=-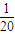 相切,且与圆x2+(y-
相切,且与圆x2+(y- )2=
)2=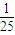 外切,建立方程,即可求动P的轨迹C的方程;
外切,建立方程,即可求动P的轨迹C的方程;
(Ⅱ)(1)求得直线L斜率,根据M,N两点不同,m2+n2=1且m≠n,可得(m+n)2<2(m2+n2)=2,即可求得结论;
(2)求出直线方程代入抛物线和椭圆方程,由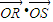 =0,求得a的范围,即可求得离心率的范围.
=0,求得a的范围,即可求得离心率的范围.
解答:解:(Ⅰ)设P(x,y),则有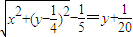 …(2分)
…(2分)
化简得:x2=y …(4分)
(II)(1)因为直线MN的斜率为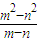 =m+n
=m+n
∵l⊥MN,m+n≠0,∴直线L斜率k=-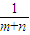 …(6分)
…(6分)
∵M,N两点不同,m2+n2=1且m≠n,∴(m+n)2<2(m2+n2)=2
∴0<|m+n|<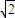
∴|k|>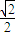
∴k<-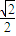 或k>
或k>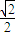 …(8分)
…(8分)
(2)l方程为:y-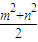 =k(x-
=k(x-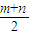 ),
),
又m2+n2=1,m+n=-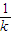 ,∴l方程为:y=kx+1代入抛物线和椭圆方程并整理得:x2-kx-1=0①;(a+2k2)x2+4kx+2-2a=0②,易知方程①的判别式
,∴l方程为:y=kx+1代入抛物线和椭圆方程并整理得:x2-kx-1=0①;(a+2k2)x2+4kx+2-2a=0②,易知方程①的判别式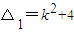 >0恒成立,方程②的判别式
>0恒成立,方程②的判别式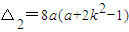
∵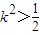 ,a>0,∴
,a>0,∴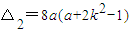 >0恒成立 …(10分)
>0恒成立 …(10分)
∵R(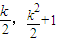 ),S(
),S(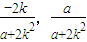 )
)
∴由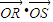 =0得-k2+a(
=0得-k2+a(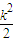 +1)=0
+1)=0
∴a= =2-
=2-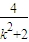 >2-
>2-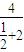 =
=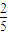
∴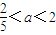
∵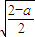 =e,∴a=2-2e2>
=e,∴a=2-2e2>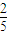
∴e2<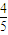
∴0<e< …(14分)
…(14分)
点评:本题考查轨迹方程,考查直线与曲线的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.
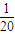 相切,且与圆x2+(y-
相切,且与圆x2+(y- )2=
)2=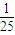 外切,建立方程,即可求动P的轨迹C的方程;
外切,建立方程,即可求动P的轨迹C的方程;(Ⅱ)(1)求得直线L斜率,根据M,N两点不同,m2+n2=1且m≠n,可得(m+n)2<2(m2+n2)=2,即可求得结论;
(2)求出直线方程代入抛物线和椭圆方程,由
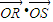 =0,求得a的范围,即可求得离心率的范围.
=0,求得a的范围,即可求得离心率的范围.解答:解:(Ⅰ)设P(x,y),则有
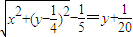 …(2分)
…(2分)化简得:x2=y …(4分)
(II)(1)因为直线MN的斜率为
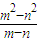 =m+n
=m+n∵l⊥MN,m+n≠0,∴直线L斜率k=-
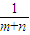 …(6分)
…(6分)∵M,N两点不同,m2+n2=1且m≠n,∴(m+n)2<2(m2+n2)=2
∴0<|m+n|<
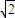
∴|k|>
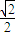
∴k<-
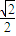 或k>
或k>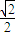 …(8分)
…(8分)(2)l方程为:y-
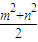 =k(x-
=k(x-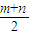 ),
),又m2+n2=1,m+n=-
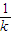 ,∴l方程为:y=kx+1代入抛物线和椭圆方程并整理得:x2-kx-1=0①;(a+2k2)x2+4kx+2-2a=0②,易知方程①的判别式
,∴l方程为:y=kx+1代入抛物线和椭圆方程并整理得:x2-kx-1=0①;(a+2k2)x2+4kx+2-2a=0②,易知方程①的判别式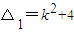 >0恒成立,方程②的判别式
>0恒成立,方程②的判别式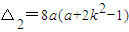
∵
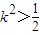 ,a>0,∴
,a>0,∴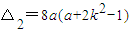 >0恒成立 …(10分)
>0恒成立 …(10分)∵R(
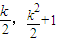 ),S(
),S(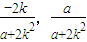 )
)∴由
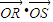 =0得-k2+a(
=0得-k2+a(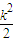 +1)=0
+1)=0∴a=
 =2-
=2-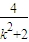 >2-
>2-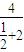 =
=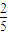
∴
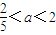
∵
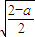 =e,∴a=2-2e2>
=e,∴a=2-2e2>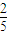
∴e2<
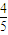
∴0<e<
 …(14分)
…(14分)点评:本题考查轨迹方程,考查直线与曲线的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目