题目内容
已知圆x2+y2=25与直线l:y=-
思路解析:根据圆和三角形相交部分的图形面积和被覆盖的比例求出未被圆覆盖部分的面积的表达式,可以借助三角函数求最值.
解:|AB|=5,圆心角∠AOB=![]() ,所以∠APB=
,所以∠APB=![]() ,S=S△PAB-S扇形=
,S=S△PAB-S扇形=
![]() (yP+
(yP+![]() )·5-
)·5-![]() (yP+
(yP+![]() )2·
)2·![]() .
.
当![]()
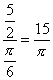 ,即
,即![]()
![]() 时,Smax
时,Smax![]() .
.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
题目内容
已知圆x2+y2=25与直线l:y=-
思路解析:根据圆和三角形相交部分的图形面积和被覆盖的比例求出未被圆覆盖部分的面积的表达式,可以借助三角函数求最值.
解:|AB|=5,圆心角∠AOB=![]() ,所以∠APB=
,所以∠APB=![]() ,S=S△PAB-S扇形=
,S=S△PAB-S扇形=
![]() (yP+
(yP+![]() )·5-
)·5-![]() (yP+
(yP+![]() )2·
)2·![]() .
.
当![]()
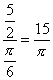 ,即
,即![]()
![]() 时,Smax
时,Smax![]() .
.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案