题目内容
已知定点N(3,0)与以点M为圆心的圆M的方程为(x+3)2+y2=16,动点P在圆M上运动,线段PN的垂直平分线交直线MP于Q点,则动点Q的轨迹方程是
-
=1
-
=1.
| x2 |
| 4 |
| y2 |
| 5 |
| x2 |
| 4 |
| y2 |
| 5 |
分析:连接QN,得出|QN|-|QM|为定值,从而可知Q满足双曲线的定义,求a、b可得它的方程.
解答: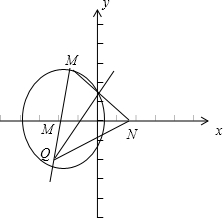 解:连接QN,如图
解:连接QN,如图
由已知,得|QN|=|QP|,所以|QN|-|QM|=|QP|-|QM|=|MP|=4
又|MN|=6,4<6,
根据双曲线的定义,点Q的轨迹是M,N为焦点,以4为实轴长的双曲线,
所以2a=4,2c=6,所以b=
,
所以,点Q的轨迹方程为:
-
=1.
故答案为:
-
=1.
 解:连接QN,如图
解:连接QN,如图由已知,得|QN|=|QP|,所以|QN|-|QM|=|QP|-|QM|=|MP|=4
又|MN|=6,4<6,
根据双曲线的定义,点Q的轨迹是M,N为焦点,以4为实轴长的双曲线,
所以2a=4,2c=6,所以b=
| 5 |
所以,点Q的轨迹方程为:
| x2 |
| 4 |
| y2 |
| 5 |
故答案为:
| x2 |
| 4 |
| y2 |
| 5 |
点评:本题主要考查了轨迹方程的问题,解题的关键是利用了双曲线的定义求得轨迹方程.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
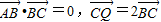 ,
,