题目内容
矩形ABCD的四个顶点的坐标分别为A(-2,1),B(2,1),C(2,-1),D(-2,-1),过原点且互相垂直的两条直线分别与矩形的边相交于E、F、G、H四点,则四边形EGFH的面积的最小值为 ,最大值为 .
【答案】分析:求出举行的各个顶点的坐标,利用两点间的距离公式求出长和宽,计算举行的面积,S=2(k+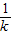 ),利用函数
),利用函数
S=2(k+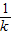 ) 在[
) 在[ ,1]上是减函数,在[1,2]上是增函数,故k=1时,S有最小值,最大值是k=
,1]上是减函数,在[1,2]上是增函数,故k=1时,S有最小值,最大值是k= 时的S值,
时的S值,
或当 k=2时的S值,计算可得答案.
解答:解:设过原点且互相垂直的两条直线分别为 y=kx,和 y=-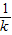 x,(不妨设k>0)由题意得,
x,(不妨设k>0)由题意得,
则 E (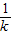 ,1),F (-
,1),F (- ,-1),G(-k,1),H(k,-1),
,-1),G(-k,1),H(k,-1),
由两点间的距离公式得 EF=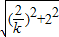 =2
=2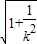 ,GH=
,GH=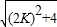 =2
=2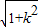 ,
,
四边形EGFH的面积为 S= •EF•GH=2
•EF•GH=2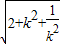 =2
=2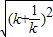 =2|
=2|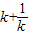 |=2(k+
|=2(k+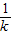 ).
).
根据E、G 两点都在线段AB上,可得-2≤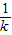 ≤2,且-2≤-k≤2,∴
≤2,且-2≤-k≤2,∴ ≤k≤2.
≤k≤2.
又函数 S=2(k+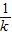 ) 在[
) 在[ ,1]上是减函数,在[1,2]上是增函数,故 k=1时,S有最小值为4.
,1]上是减函数,在[1,2]上是增函数,故 k=1时,S有最小值为4.
当 k= 时,S=5; 当 k=2时,S=5. 当 k=0时,S=4.
时,S=5; 当 k=2时,S=5. 当 k=0时,S=4.
综上,S的最小值等于4,最大值等于 5,
故答案为 4,5.
点评:本题考查函数的单调性及函数的最值,两直线垂直的性质,体现了数形结合的数学思想,其中,确定一直线的斜率
k的范围是解题的关键和难点.
 ),利用函数
),利用函数 S=2(k+
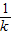 ) 在[
) 在[ ,1]上是减函数,在[1,2]上是增函数,故k=1时,S有最小值,最大值是k=
,1]上是减函数,在[1,2]上是增函数,故k=1时,S有最小值,最大值是k= 时的S值,
时的S值,或当 k=2时的S值,计算可得答案.
解答:解:设过原点且互相垂直的两条直线分别为 y=kx,和 y=-
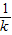 x,(不妨设k>0)由题意得,
x,(不妨设k>0)由题意得,则 E (
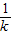 ,1),F (-
,1),F (- ,-1),G(-k,1),H(k,-1),
,-1),G(-k,1),H(k,-1),由两点间的距离公式得 EF=
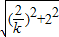 =2
=2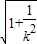 ,GH=
,GH=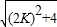 =2
=2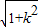 ,
,四边形EGFH的面积为 S=
 •EF•GH=2
•EF•GH=2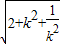 =2
=2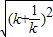 =2|
=2|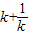 |=2(k+
|=2(k+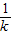 ).
).根据E、G 两点都在线段AB上,可得-2≤
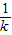 ≤2,且-2≤-k≤2,∴
≤2,且-2≤-k≤2,∴ ≤k≤2.
≤k≤2.又函数 S=2(k+
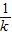 ) 在[
) 在[ ,1]上是减函数,在[1,2]上是增函数,故 k=1时,S有最小值为4.
,1]上是减函数,在[1,2]上是增函数,故 k=1时,S有最小值为4.当 k=
 时,S=5; 当 k=2时,S=5. 当 k=0时,S=4.
时,S=5; 当 k=2时,S=5. 当 k=0时,S=4.综上,S的最小值等于4,最大值等于 5,
故答案为 4,5.

点评:本题考查函数的单调性及函数的最值,两直线垂直的性质,体现了数形结合的数学思想,其中,确定一直线的斜率
k的范围是解题的关键和难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
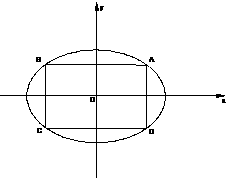 如图:在椭圆
如图:在椭圆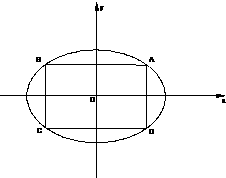
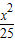 +
+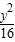 =1中有一内接矩形ABCD(四个顶点都在椭圆上),A点在第一象限内.当内接矩形ABCD的面积最大时,点A的坐标是( )
=1中有一内接矩形ABCD(四个顶点都在椭圆上),A点在第一象限内.当内接矩形ABCD的面积最大时,点A的坐标是( )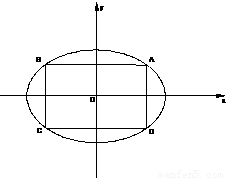
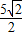 ,2
,2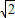 )
) ,2)
,2)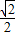 ,
,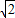 )
)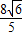 )
)