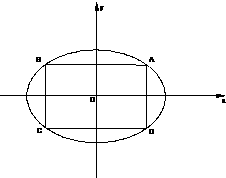
题目内容
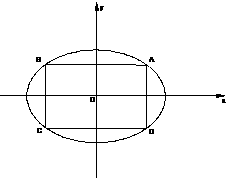 如图:在椭圆
如图:在椭圆| x2 |
| 25 |
| y2 |
| 16 |
分析:先根据椭圆参数方程设出A点坐标,则椭圆
+
=1的内接矩形ABCD的面积可用A点坐标表示,就把矩形ABCD的面积用含参数θ的式子表示,再利用正弦函数的有界性判断θ为何值时,面积有最大值.
| x2 |
| 25 |
| y2 |
| 16 |
解答:解:∵A点在椭圆
+
=1上,∴可设A(5cosθ,4sinθ)
∴矩形ABCD的面积为4×(5cosθ)(4sinθ)=80cosθsinθ=40sin2θ
∵sin2θ≤1,且当2θ=
时等号成立,
∴40sin2θ≤40,且当2θ=
时等号成立,
∴当2θ=
,即θ=
时,椭圆
+
=1的内接矩形ABCD面积有最大值,此时A(
,2
)
故选A
| x2 |
| 25 |
| y2 |
| 16 |
∴矩形ABCD的面积为4×(5cosθ)(4sinθ)=80cosθsinθ=40sin2θ
∵sin2θ≤1,且当2θ=
| π |
| 2 |
∴40sin2θ≤40,且当2θ=
| π |
| 2 |
∴当2θ=
| π |
| 2 |
| π |
| 4 |
| x2 |
| 25 |
| y2 |
| 16 |
5
| ||
| 2 |
| 2 |
故选A
点评:本题主要考查椭圆的参数方程在求最值时的应用,其中结合了三角函数的有界性,属于综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知点P为椭圆
如图,已知点P为椭圆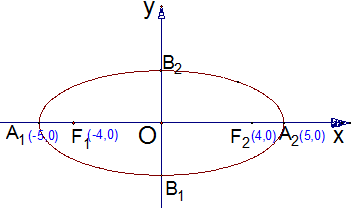 如图,A1,A为椭圆的两个顶点,F1,F2为椭圆的两个焦点.
如图,A1,A为椭圆的两个顶点,F1,F2为椭圆的两个焦点. (2003•北京)如图,A1,A为椭圆的两个顶点,F1,F2为椭圆的两个焦点.
(2003•北京)如图,A1,A为椭圆的两个顶点,F1,F2为椭圆的两个焦点.