题目内容
已知:等差数列{an}中,a4=14,前10项和S10=185.
(Ⅰ)求an;
(Ⅱ)将{an}中的第2项,第4项,…,第2n项按原来的顺序排成一个新数列,求此数列的前n项和Gn.
解:(Ⅰ)由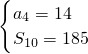
∴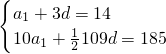 ,
,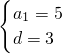 …(3分)
…(3分)
由an=5+(n-1)•3∴an=3n+2…(6分)
(Ⅱ)设新数列为{bn},由已知,bn=3•2n+2…(9分)
∴Gn=3(21+22+23+…+2n)+2n=6(2n-1)+2n.
∴Gn=3•2n+1+2n-6,(n∈N*)…(12分)
分析:(Ⅰ)根据题意,利用等差数列的通项公式与求和公式将a4与s10列方程组即可求得其首项与公差,从而可求得an;
(Ⅱ)根据题意,新数列为{bn}的通项为bn=3•2n+2,利用分组求和的方法即可求得Gn.
点评:本题考查数列的通项与求和,重点考查等差数列的通项公式与求和公式及分组求和法的应用,是基础题.
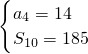
∴
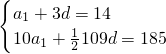 ,
,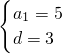 …(3分)
…(3分)由an=5+(n-1)•3∴an=3n+2…(6分)
(Ⅱ)设新数列为{bn},由已知,bn=3•2n+2…(9分)
∴Gn=3(21+22+23+…+2n)+2n=6(2n-1)+2n.
∴Gn=3•2n+1+2n-6,(n∈N*)…(12分)
分析:(Ⅰ)根据题意,利用等差数列的通项公式与求和公式将a4与s10列方程组即可求得其首项与公差,从而可求得an;
(Ⅱ)根据题意,新数列为{bn}的通项为bn=3•2n+2,利用分组求和的方法即可求得Gn.
点评:本题考查数列的通项与求和,重点考查等差数列的通项公式与求和公式及分组求和法的应用,是基础题.

练习册系列答案
相关题目
已知在等差数列{an}中,a1=120,d=-4,若Sn≤an(n≥2),则n的最小值为( )
| A、60 | B、62 | C、70 | D、72 |