题目内容
已知递增等差数列{an}满足:a1=1,且a1,a2,a4成等比数列.
(1)求数列{an}的通项公式an;
(2)若不等式(1-
)•(1-
)…(1-
)≤
对任意n∈N+,试猜想出实数m小值,并证明.
(1)求数列{an}的通项公式an;
(2)若不等式(1-
| 1 |
| 2a1 |
| 1 |
| 2a2 |
| 1 |
| 2an |
| m | ||
|
分析:(1)设数列{an}公差为d(d>0),由a1,a2,a4成等比数列可求得d,从而可求得数列{an}的通项公式an;
(2)由(1)得an=n,可将原不等式转化为
•
•
…
≤
,利用n=1与n=2即可猜想m的最小值为
,利用数学归纳法证明即可.
(2)由(1)得an=n,可将原不等式转化为
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 2n-1 |
| 2n |
| m | ||
|
| ||
| 2 |
解答:解:(1)设数列{an}公差为d(d>0),
由题意可知a1•a4=a22,即1(1+3d)=(1+d)2,
解得d=1或d=0(舍去).
所以,an=1+(n-1)•1=n.
(2)不等式等价于
•
•
…
≤
,
当n=1时,m≥
;当n=2时,m≥
;
而
>
,所以猜想,m的最小值为
.
下证不等式
•
•
…
≤
对任意n∈N*恒成立.
下面用数学归纳法证明.
证明:1°当n=1时,
≤
=
,成立.
2°假设当n=k时,不等式,
•
•
…
≤
成立,
当n=k+1时,
•
•
…
•
≤
•
,
只要证
•
≤
,
只要证
≤
,
只要证
-
≤2k+2,
只要证4k2+8k+3≤4k2+8k+4,
只要证3≤4,显然成立.
所以,对任意n∈N*,不等式
•
•
…
≤
恒成立.
由题意可知a1•a4=a22,即1(1+3d)=(1+d)2,
解得d=1或d=0(舍去).
所以,an=1+(n-1)•1=n.
(2)不等式等价于
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 2n-1 |
| 2n |
| m | ||
|
当n=1时,m≥
| ||
| 2 |
3
| ||
| 8 |
而
| ||
| 2 |
3
| ||
| 8 |
| ||
| 2 |
下证不等式
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 2n-1 |
| 2n |
| ||||
|
下面用数学归纳法证明.
证明:1°当n=1时,
| 1 |
| 2 |
| ||||
|
| 1 |
| 2 |
2°假设当n=k时,不等式,
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 2k-1 |
| 2k |
| ||||
|
当n=k+1时,
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 2k-1 |
| 2k |
| 2k+1 |
| 2k+2 |
| ||||
|
| 2k+1 |
| 2k+2 |
只要证
| ||||
|
| 2k+1 |
| 2k+2 |
| ||||
|
只要证
| ||
|
| 1 | ||
|
只要证
| 2k+1 |
| 2k+3 |
只要证4k2+8k+3≤4k2+8k+4,
只要证3≤4,显然成立.
所以,对任意n∈N*,不等式
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 2n-1 |
| 2n |
| ||||
|
点评:本题考查数学归纳法,考查等差数列的通项公式,考查猜想与推理证明的能力,猜想出m的值是关键,也是难点,属于难题.

练习册系列答案
相关题目
 .
. 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值.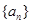 中,
中,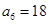 且
且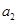 是
是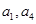 的等比中项,则它的第4项到第11项的和为
的等比中项,则它的第4项到第11项的和为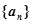 ,满足
,满足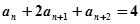 ,则该数列为( )
,则该数列为( )