题目内容
【题目】如图,在四棱锥![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 中点.
中点.
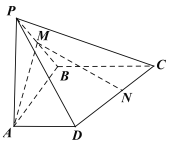
(1)已知点![]() 在棱
在棱![]() 上,且平面
上,且平面![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置并说明理由;
的位置并说明理由;
(2)设点![]() 是线段
是线段![]() 上的动点,当点
上的动点,当点![]() 在何处时,直线
在何处时,直线![]() 与平面
与平面![]() 所成角最大?并求最大角的正弦值.
所成角最大?并求最大角的正弦值.
【答案】(1)![]() 为
为![]() 中点,理由见解析;(2)当点
中点,理由见解析;(2)当点![]() 在线段
在线段![]() 靠近
靠近![]() 的三等分点时,直线
的三等分点时,直线![]() 与平面
与平面![]() 所成角最大,最大角的正弦值
所成角最大,最大角的正弦值![]() .
.
【解析】
(1)![]() 为
为![]() 中点,可利用中位线与平行四边形性质证明
中点,可利用中位线与平行四边形性质证明![]() ,
,![]() ,从而证明平面
,从而证明平面![]() 平面
平面![]() ;
;
(2)以A为原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系,利用向量法求出当点
轴建立空间直角坐标系,利用向量法求出当点![]() 在线段
在线段![]() 靠近
靠近![]() 的三等分点时,直线
的三等分点时,直线![]() 与平面
与平面![]() 所成角最大,并可求出最大角的正弦值.
所成角最大,并可求出最大角的正弦值.
(1)![]() 为
为![]() 中点,证明如下:
中点,证明如下:
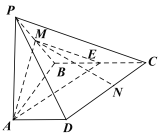
![]()
![]() 分别为
分别为![]() 中点,
中点,
![]()
又![]() 平面
平面![]() 平面
平面![]()
![]() 平面
平面![]()
又![]() ,且
,且![]()
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]()
同理,![]() 平面
平面![]() ,又
,又![]()
![]() 平面
平面![]() 平面
平面![]()
(2)以A为原点,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 、
、![]() 、
、![]() 轴建立空间直角坐标系
轴建立空间直角坐标系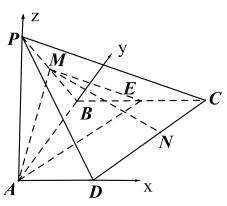
则![]() ,
,![]()
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,![]() 则
则
![]()
取平面![]() 的法向量为
的法向量为![]() 则
则
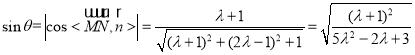
令![]() ,则
,则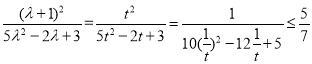
所以![]()
当![]() 时,等号成立
时,等号成立
即当点![]() 在线段
在线段![]() 靠近
靠近![]() 的三等分点时,直线
的三等分点时,直线![]() 与平面
与平面![]() 所成角最大,最大角的正弦值
所成角最大,最大角的正弦值![]() .
.

【题目】我校随机抽取100名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作 | 不太主动参加班级工作 | 总计 | |
学习积极性高 | 40 | ||
学习积极性一般 | 30 | ||
总计 | 100 |
已知随机抽查这100名学生中的一名学生,抽到积极参加班级工作的学生的概率是0.6.
(1)请将上表补充完整(不用写计算过程);
(2)试运用独立性检验的思想方法学生的学习积极性与对待班级工作的态度是否有关?并说明理由.附:
| 0.050 | 0.010 | 0.001 |
K | 3.841 | 6.635 | 10.828 |
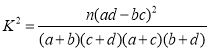
【题目】某市环保部门对该市市民进行了一次垃圾分类知识的网络问卷调查,每位市民仅有一次参加机会,通过随机抽样,得到参与问卷调查的100人的得分(满分:100分)数据,统计结果如表所示:
组别 |
|
|
|
|
|
|
男 | 2 | 3 | 5 | 15 | 18 | 12 |
女 | 0 | 5 | 10 | 10 | 7 | 13 |
(1)若规定问卷得分不低于70分的市民称为“环保关注者”,请完成答题卡中的![]() 列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否为“环保关注者”与性别有关?
列联表,并判断能否在犯错误概率不超过0.05的前提下,认为是否为“环保关注者”与性别有关?
(2)若问卷得分不低于80分的人称为“环保达人”.视频率为概率.
①在我市所有“环保达人”中,随机抽取3人,求抽取的3人中,既有男“环保达人”又有女“环保达人”的概率;
②为了鼓励市民关注环保,针对此次的调查制定了如下奖励方案:“环保达人”获得两次抽奖活动;其他参与的市民获得一次抽奖活动.每次抽奖获得红包的金额和对应的概率.如下表:
红包金额(单位:元) | 10 | 20 |
概率 |
|
|
现某市民要参加此次问卷调查,记![]() (单位:元)为该市民参加间卷调查获得的红包金额,求
(单位:元)为该市民参加间卷调查获得的红包金额,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】2020年春季,某出租汽车公司决定更换一批新的小汽车以代替原来报废的出租车,现有![]() 两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
两款车型,根据以往这两种出租车车型的数据,得到两款出租车车型使用寿命频数表如下:
使用寿命年数 | 5年 | 6年 | 7年 | 8年 | 总计 |
| 10 | 20 | 45 | 25 | 100 |
| 15 | 35 | 40 | 10 | 100 |
(1)填写下表,并判断是否有![]() 的把握认为出租车的使用寿命年数与汽车车型有关?
的把握认为出租车的使用寿命年数与汽车车型有关?
使用寿命不高于 | 使用寿命不低于 | 总计 | |
| |||
| |||
总计 |
(2)司机师傅小李准备在一辆开了![]() 年的
年的![]() 型车和一辆开了
型车和一辆开了![]() 年的
年的![]() 型车中选择,为了尽最大可能实现
型车中选择,为了尽最大可能实现![]() 年内(含
年内(含![]() 年)不换车,试通过计算说明,他应如何选择.
年)不换车,试通过计算说明,他应如何选择.
附: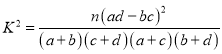 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |