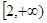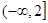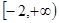题目内容
若a>0,b>0,c>0,a(a+b+c)+bc=4-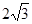 ,则2a+b+c的最小值是 .
,则2a+b+c的最小值是 .
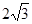 ,则2a+b+c的最小值是 .
,则2a+b+c的最小值是 .. 2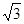 -2
-2
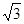 -2
-2 解:若a,b,c>0且a(a+b+c)+bc=4-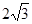 ,
,
所以a2+ab+ac+bc=4-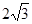 ,4-
,4-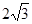 =a2+ab+ac+bc="1/" 4 (4a2+4ab+4ac+2bc+2bc)≤1/ 4 (4a2+4ab+4ac+2bc+b2+c2),∴(
=a2+ab+ac+bc="1/" 4 (4a2+4ab+4ac+2bc+2bc)≤1/ 4 (4a2+4ab+4ac+2bc+b2+c2),∴(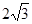 -2)2≤(2a+b+c)2,
-2)2≤(2a+b+c)2,
则(2a+b+c)≥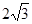 -2,
-2,
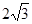 ,
,所以a2+ab+ac+bc=4-
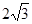 ,4-
,4-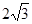 =a2+ab+ac+bc="1/" 4 (4a2+4ab+4ac+2bc+2bc)≤1/ 4 (4a2+4ab+4ac+2bc+b2+c2),∴(
=a2+ab+ac+bc="1/" 4 (4a2+4ab+4ac+2bc+2bc)≤1/ 4 (4a2+4ab+4ac+2bc+b2+c2),∴(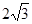 -2)2≤(2a+b+c)2,
-2)2≤(2a+b+c)2,则(2a+b+c)≥
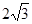 -2,
-2,
练习册系列答案
相关题目
 中
中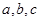 分别为角
分别为角 所对的边的边长,
所对的边的边长, ,求证:
,求证: .
.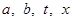 都是实数,且
都是实数,且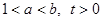 ,
,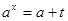 ,则
,则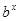 与
与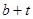 的大小关系是
的大小关系是






 (其中k为常数),且z=x+3y的最大值为12,则k的值等于 .
(其中k为常数),且z=x+3y的最大值为12,则k的值等于 . 满足:
满足: ,其中
,其中 ,又已知
,又已知 ,
, .
. ,求
,求 的表达式;
的表达式;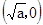 ,记
,记 ,且
,且 成立,试求a的取值范围;
成立,试求a的取值范围; 的前n项和为
的前n项和为 ,试求:
,试求: 。
。 对
对 恒成立,则实数
恒成立,则实数 的取值范围是 .
的取值范围是 . 能成立,则实数
能成立,则实数 的取值范围是
的取值范围是




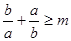 恒成立,则m的取值范围是( ).
恒成立,则m的取值范围是( ).