题目内容
若
，
，
是空间任意三个向量，λ∈R，下列关系式中，不成立的是（ ）
| a |
| b |
| c |
分析：直接根据向量的交换律可判定选项A，根据向量具有数乘的分配律可判定选项B，根据向量的结合律可判定选项C，
，
不一定共线可判定选项D．
| a |
| b |
解答：解：选项A，根据向量的交换律可知正确；
选项B，向量具有数乘的分配律，可知正确；
选项C，根据向量的结合律可知正确；
选项D，
，
不一定共线，故D不正确
故选D．
选项B，向量具有数乘的分配律，可知正确；
选项C，根据向量的结合律可知正确；
选项D，
| a |
| b |
故选D．
点评：本题主要考查了平行向量与共线向量，以及向量的运算律，属于基础题．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
若向量
，
，
的起点与终点M、A、B、C互不重合且无三点共线，且满足下列关系（O为空间任一点），则能使向量
，
，
成为空间一组基底的关系是（ ）
| MA |
| MB |
| MC |
| MA |
| MB |
| MC |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、
| ||||||||||||||
D、
|
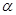//平面
，
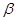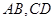是夹在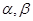
间的线段，若
//
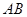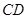，则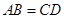
；
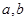是异面直线，
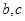是异面直线，则
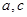一定是异面直线；
，
//
；
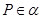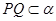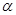//平面
，
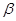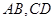是夹在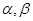
间的线段，若
//
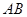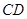，则
；
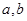是异面直线，
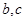是异面直线，则
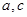一定是异面直线；
，
//
；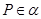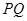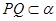