题目内容
设函数 对任意实数x 、y都有
对任意实数x 、y都有 ,
,
(1)求 的值;
的值;
(2)若 ,求
,求 、
、 、
、 的值;
的值;
(3)在(2)的条件下,猜想
 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。
(1)0 (2)4,9,16 (3)
解析试题分析:(1)令x=y=0得f(0+0)=f(0)+f(0)+2×0×0⇒f(0)=0
(2)f(1)=1, f(2)=f(1+1)=1+1+2=4 f(3)=f(2+1)=4+1+2×2×1=9 f(4)=f(3+1)=9+1+2×3×1=16
(3)猜想f(n)= ,下用数学归纳法证明之.
,下用数学归纳法证明之.
当n=1时,f(1)=1满足条件
假设当n=k时成立,即f(k)=
则当n=k+1时f(k+1)=f(k)+f(1)+2k= +1+2k=(k+1)
+1+2k=(k+1)
从而可得当n=k+1时满足条件
对任意的正整数n,都有 f(n)=
考点:抽象函数及其应用
点评:本题目主要考查了利用赋值法求解抽象函数的函数值,及数学归纳法在证明数学命题中的应用,及利用放缩法证明不等式等知识的综合.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
若 ,则复数
,则复数 =( )
=( )
A. | B. | C. | D.5 |
已知 是虚数单位,
是虚数单位, ,则
,则 =( )
=( )
A. | B.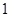 | C. | D. |
已知复数 满足
满足 ,则
,则 的模
的模 等于( )
等于( )
A. | B. | C. | D.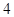 |


 ,
, x3-x,数列{an}满足条件:a1≥1,an+1≥f'(an+1).试比较
x3-x,数列{an}满足条件:a1≥1,an+1≥f'(an+1).试比较 +
+ +
+ +…+
+…+ 与1的大小,并说明理由.
与1的大小,并说明理由.

 在点
在点 处的切线斜率为
处的切线斜率为 ,且
,且 .对一切实数
.对一切实数 ,不等式
,不等式 恒成立(
恒成立( ≠0).
≠0). 的值;
的值; >
> .
. 中,
中, 、
、 ,且
,且 .
. 、
、 ,猜想
,猜想 的表达式,并加以证明;
的表达式,并加以证明; ,求证:对任意的自然数
,求证:对任意的自然数 ,都有
,都有 .
.