题目内容
设曲线 在点
在点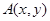 处的切线斜率为
处的切线斜率为 ,且
,且 .对一切实数
.对一切实数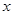 ,不等式
,不等式 恒成立(
恒成立( ≠0).
≠0).
(1) 求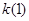 的值;
的值;
(2) 求函数 的表达式;
的表达式;
(3) 求证: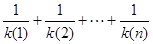 >
> .
.
(1) 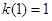 (2)
(2)  (3)
(3) 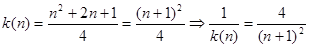 要证原不等式,即证
要证原不等式,即证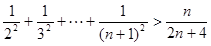 因为
因为
所以
 =
= 所以
所以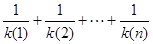

解析试题分析:(1)由 ,所以
,所以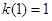 2分
2分
(2) ,由
,由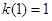 ,
,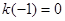 得 3分
得 3分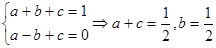 4分
4分
又 恒成立,则由
恒成立,则由 恒成立得
恒成立得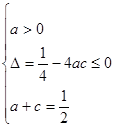
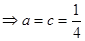 , 6分
, 6分
同理由 恒成立也可得:
恒成立也可得:  7分
7分
综上 ,
, ,所以
,所以 8分
8分
(3)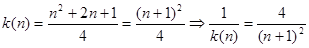
要证原不等式,即证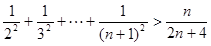
因为
所以
 =
=
所以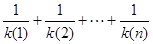
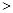
 12分
12分
本小问也可用数学归纳法求证。证明如下:
由
当 时,左边=1,右边=
时,左边=1,右边= ,左边>右边,所以
,左边>右边,所以 ,不等式成立
,不等式成立
假设当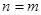 时,不等式成立,即
时,不等式成立,即
当 时,
时,
左边=

由
所以
即当 时,不等式也成立。综上得
时,不等式也成立。综上得 
考点:函数导数,求函数解析式及不等式证明
点评:函数求解析式采用的是待定系数法,由已知条件找到 的关系式,期间将不等式恒成立问题转化为二次函数性质的考察,第三问在证明不等式时用到了放缩法,这种方法对学生有一定的难度
的关系式,期间将不等式恒成立问题转化为二次函数性质的考察,第三问在证明不等式时用到了放缩法,这种方法对学生有一定的难度

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
复数 等于( )
等于( )
A. | B. | C.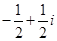 | D. |
已知 为纯虚数,
为纯虚数,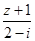 是实数,那么
是实数,那么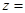 ( )
( )
A.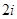 | B. | C.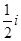 | D. |
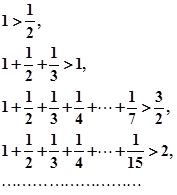

 .
.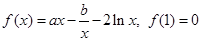
 在其定义域上为单调函数,求
在其定义域上为单调函数,求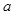 的取值范围;
的取值范围;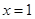 处的切线的斜率为0,
处的切线的斜率为0, ,已知
,已知 求证:
求证:
 与
与 的大小,并说明理由.
的大小,并说明理由. 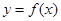 对任意实数x 、y都有
对任意实数x 、y都有 ,
,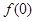 的值;
的值;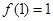 ,求
,求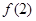 、
、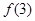 、
、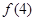 的值;
的值;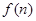
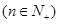 的表达式,并用数学归纳法加以证明。
的表达式,并用数学归纳法加以证明。 …
…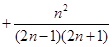 =
=
 都成立.
都成立.