题目内容

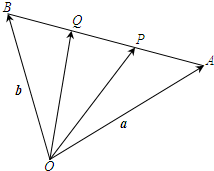精英家教网如图，设点P、Q是线段AB的三等分点，若
OA
=a，
OB
=b，则
OP
=（　　）用a、b表示．
A、-
2
3
a
+
1
3
b
B、
1
3
b
+
2
3
a
C、
1
2
a
+
1
3
b
D、
1
3
a
-
2
3
b
分析：由已知
OA
=a，
OB
=b，及向量加法的三角形法可得
OP
=
OA
+
AP
=
OA
+
1
3
AB
=
OA
+
1
3
(
OB
-
OA
)=
1
3
OB
+
2
3
OA
，把已知代入可求．
解答：解：∵
OA
=a，
OB
=b，
由向量加法的三角形法则可得
OP
=
OA
+
AP
=
OA
+
1
3
AB

=
OA
+
1
3
(
OB
-
OA
)
=
1
3
OB
+
2
3
OA

=
1
3
b
+
2
3
a

故选B．
点评：本题主要注意灵活应用向量加法，减法的三角形法则及向量共线定理，灵活利用向量的知识是解决本题的关键．
练习册系列答案
相关题目
精英家教网在平面向量中有如下定理：设点O、P、Q、R为同一平面内的点，则P、Q、R三点共线的充要条件是：存在实数t，使
OP
=(1-t)
OQ
+t
OR
．试利用该定理解答下列问题：
如图，在△ABC中，点E为AB边的中点，点F在AC边上，且CF=2FA，BF交CE于点M，设
AM
=x
AE
+y
AF
，则x+2y=
 
．
（2011•惠州二模）在平面向量中有如下定理：设点O，P，Q，R为同一平面内的点，则P，Q，R三点共线的充要条件是：存在实数t，使
OP
=(1-t)
OQ
+t
OR
．如图，在△ABC中，点E为AB边的中点，点F在AC边上，且CF=2FA，BF交CE于点M，设
AM
=x
AE
+y
AF
，则（　　）
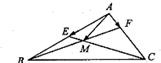
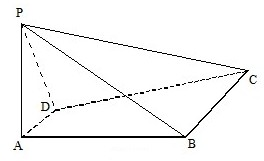精英家教网如图，四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD是直角梯形，其中DA⊥AB，AD∥BC．PA=2AD=BC=2AB=2
2
．
（1）求异面直线PC与AD所成角的大小；
（2）若平面ABCD内有一经过点C的曲线E，该曲线上的任一动点Q都满足PQ与AD所成角的大小恰等PC与AD所成角．试判断曲线E的形状并说明理由；
（3）在平面ABCD内，设点Q是（2）题中的曲线E在直角梯形ABCD内部（包括边界）的一段曲线CG上的动点，其中G为曲线E和DC的交点．以B为圆心，BQ为半径的圆分别与梯形的边AB、BC交于M、N两点．当Q点在曲线段GC上运动时，试提出一个研究有关四面P-BMN的问题（如体积、线面、面面关系等）并尝试解决．
（说明：本小题将根据你提出的问题的质量和解决难度分层评分；本小题的计算结果可以使用近似值，保留3位小数）

在平面向量中有如下定理：设点O，P，Q，R为同一平面内的点，则P、Q、R三点共线的充要条件是：存在实数t，使.试利用该定理解答下列问题：

如图，在ΔABC中，点E为AB边的中点，点F在AC边上，且CF＝2FA，BF交CE于点M，设，则x＋y＝      

在平面向量中有如下定理：设点O，P，Q，R为同一平面内的点，则P、Q、R三点共线的充要条件是：存在实数t，使.试利用该定理解答下列问题：如图，

 


在ΔABC中，点E为AB边的中点，点F在AC边上，且CF＝2FA，BF交CE于点M，设，则x＋y＝     .

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网