题目内容
在一条笔直的工艺流水线上有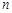 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图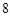 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为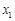 ,
,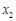 ,
, ,
, ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
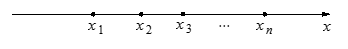
(Ⅰ)若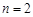 ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置;
(Ⅱ)若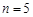 ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为 ,
,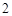 ,
,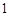 ,
,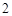 ,
,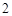 ,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
【答案】
(Ⅰ)设供应站坐标为 ,根据两点间距离最短,列出各工作台上的所有工人到供应站的距离之和为
,根据两点间距离最短,列出各工作台上的所有工人到供应站的距离之和为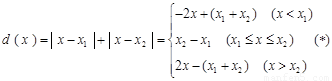 ,然后分段讨论,去掉绝对值符号,化为分段函数,求函数
,然后分段讨论,去掉绝对值符号,化为分段函数,求函数 取最小值满足的条件即可.(Ⅱ)同(Ⅰ)首先列出各工作台上的所有工人到供应站的距离之和为
取最小值满足的条件即可.(Ⅱ)同(Ⅰ)首先列出各工作台上的所有工人到供应站的距离之和为 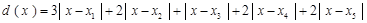 ,然后分段讨论,去掉绝对值符号,化为分段函数,求函数
,然后分段讨论,去掉绝对值符号,化为分段函数,求函数 取最小值满足的条件即可.
取最小值满足的条件即可.
【解析】
试题分析:设供应站坐标为 ,各工作台上的所有工人到供应站的距离之和为
,各工作台上的所有工人到供应站的距离之和为 .
.
(Ⅰ) 2分
2分
当 时,
时,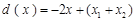 在区间
在区间 上是减函数;
上是减函数;
当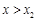 时,
时, 在区间
在区间 上是增函数.
上是增函数.
则当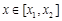 时,
时, 式取最小值,即供应站的位置为
式取最小值,即供应站的位置为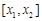 内的任意一点.
内的任意一点.  分
分
(Ⅱ)由题设知,各工作台上的所有工人到供应站的距离之和为
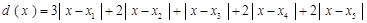 .
7分
.
7分
类似于(Ⅰ)的讨论知,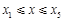 ,且有
,且有
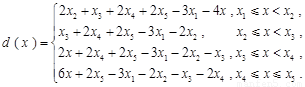
 分
分
所以,函数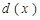 在区间
在区间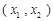 上是减函数,在区间
上是减函数,在区间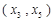 上是增函数,在区间
上是增函数,在区间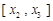 上是常数.故供应站位置位于区间
上是常数.故供应站位置位于区间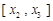 上任意一点时,均能使函数
上任意一点时,均能使函数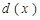 取得最小值,且最小值为
取得最小值,且最小值为 .
13分
.
13分
考点:综合运用函数知识解决实际问题的能力

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
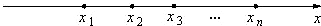
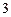 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图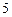 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为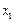 ,
, ,
,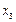 ,每个工作台上有若干名工人.现要在
,每个工作台上有若干名工人.现要在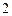 ,
,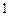 ,
,
 ,每个工作台上有若干名工人.现要在
,每个工作台上有若干名工人.现要在 与
与 之间修建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
之间修建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为 ,
, ,
, ,
, ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短. ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置; ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为 ,
, ,
, ,
,