题目内容
给出下列四个命题
①p:x>3,q:x>4,¬p是¬q的充分不必要条件;
②x=-1为函数f(x)=x+lnx的一个极值点;
③函数f(x)=|tanx|的最小正周期为
;
④(-
,0)是函数f(x)=sinx+cosx的一个对称中心.
其中正确命题的序号是( )
①p:x>3,q:x>4,¬p是¬q的充分不必要条件;
②x=-1为函数f(x)=x+lnx的一个极值点;
③函数f(x)=|tanx|的最小正周期为
| π |
| 2 |
④(-
| π |
| 4 |
其中正确命题的序号是( )
分析:①可求得条件¬p与 条件¬q,利用充分不必要条件的定义判断即可;
②先考查定义域,再判断;
③函数f(x)=|tanx|的最小正周期仍为π,从而可判断其正误;
④用辅助角公式将f(x)=sinx+cosx化为f(x)=
sin(x+
),f(-
)=0,可判断其正确.
②先考查定义域,再判断;
③函数f(x)=|tanx|的最小正周期仍为π,从而可判断其正误;
④用辅助角公式将f(x)=sinx+cosx化为f(x)=
| 2 |
| π |
| 4 |
| π |
| 4 |
解答:解:①¬p:x≤3,¬q:x≤4,显然¬p是¬q的充分不必要条件,正确;
②x=-1不在函数f(x)=x+lnx的定义域内,错;
③函数f(x)=|tanx|的最小正周期为π,错;
④f(x)=sinx+cosx=
sin(x+
),显然(-
,0)是函数f(x)的一个对称中心,正确.
故选D.
②x=-1不在函数f(x)=x+lnx的定义域内,错;
③函数f(x)=|tanx|的最小正周期为π,错;
④f(x)=sinx+cosx=
| 2 |
| π |
| 4 |
| π |
| 4 |
故选D.
点评:本题考查必要条件、充分条件与充要条件的判断,考查正弦函数的性质,考查利用导数研究函数的极值,覆盖面广,综合性强,属于中档题.

练习册系列答案
相关题目
 在区间
在区间 内存在零点,命题q:存在负数x使得
内存在零点,命题q:存在负数x使得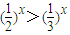 ,给出下列四个命题①p或q;②p且q;③p的否定;④q的否定,真命题的个数是( )
,给出下列四个命题①p或q;②p且q;③p的否定;④q的否定,真命题的个数是( ) 在区间
在区间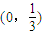 内存在零点,命题q:存在负数x使得
内存在零点,命题q:存在负数x使得 ,给出下列四个命题①p或q;②p且q;③p的否定;④q的否定,真命题的个数是( )
,给出下列四个命题①p或q;②p且q;③p的否定;④q的否定,真命题的个数是( )