题目内容
已知命题：p：函数f(x)=(
)x-log
x在区间(0，
)内存在零点，命题q：存在负数x使得(
)x＞(
)x，给出下列四个命题①p或q；②p且q；③p的否定；④q的否定，真命题的个数是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| A、1 | B、2 | C、3 | D、4 |
分析：在区间(0，
)内，(
)x＜(
)0=1；在区间(0，
)内，log
x＞log
=1．所以在区间(0，
)内，函数f(x)=(
)x-log
x＜0，即不存在零点，而由y=(
)x与y=(
)x的图象可知，当x＜0时，总有(
)x＜(
)x．因此p、q均为假命题，最后根据复合命题的真假表即可作出判断．
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
解答：解：因为函数y=(
)x在区间(0，
)上为减函数，所以(
)x＜1；
又因为函数y=log
x在区间(0，
)上也为减函数，所以log
x＞1．
因此函数f(x)=(
)x-log
x在区间(0，
)内恒小于零，即不存在零点，所以命题p是假命题．
当x＜0时，总有(
)x＜(
)x，所以命题q是假命题．
由此可知①②是假命题，③④是真命题．
故选B．
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
又因为函数y=log
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
因此函数f(x)=(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
当x＜0时，总有(
| 1 |
| 2 |
| 1 |
| 3 |
由此可知①②是假命题，③④是真命题．
故选B．
点评：本题考查复合命题的真假情况，同时考查指数函数与对数函数的图象、单调性、特殊点等．
练习册系列答案
相关题目
已知命题：p：函数f（x）=sinxcosx的最小正周期为π；命题q：函数g(x)=sin(x+
)的图象关于原点对称，则下列命题中为真命题的是（ ）
| π |
| 2 |
| A、p∧q | B、p∨q |
| C、?p | D、（?p）∨q |
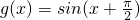的图象关于原点对称，则下列命题中为真命题的是
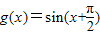的图象关于原点对称，则下列命题中为真命题的是（ ）