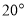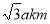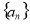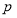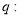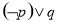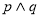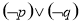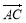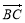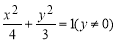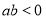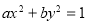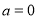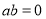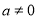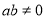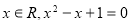题目内容
如图,椭圆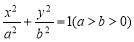 过点P(1,
过点P(1, 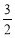 ),其左、右焦点分别为F1,F2,离心率e=
),其左、右焦点分别为F1,F2,离心率e=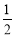 ,M,N是直线x=4上的两个动点,且
,M,N是直线x=4上的两个动点,且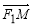 ·
·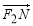 =0.
=0.
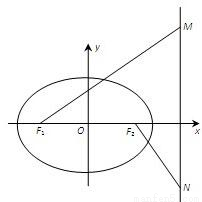
(1)求椭圆的方程;
(2)求|MN|的最小值;
(3)以MN为直径的圆C是否过定点?请证明你的结论。
(1)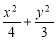 =1;(2)
=1;(2)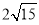 ;(3)(4-
;(3)(4-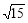 ,0)和(4+
,0)和(4+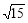 ,0) .
,0) .
【解析】
试题分析:(1)因为: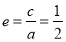 ,且过点P(1,
,且过点P(1, 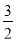 ),列出关于a,b的方程,解得a,b.最后写出椭圆方程即可;(2)设点M(4,m),N(4,n)写出向量的坐标,利用向量的数量积得到mn=-15,又|MN|=|m-n|=|m|+|n|=|m|+
),列出关于a,b的方程,解得a,b.最后写出椭圆方程即可;(2)设点M(4,m),N(4,n)写出向量的坐标,利用向量的数量积得到mn=-15,又|MN|=|m-n|=|m|+|n|=|m|+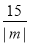 ≥
≥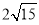 ,结合基本不等式即可求得MN的最小值;
,结合基本不等式即可求得MN的最小值;
(3)利用圆心C的坐标和半径得出圆C的方程,再令y=0,得x2-8x+1=0从而得出圆C过定点.
试题解析:(1)由已知可得
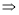
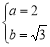
∴椭圆的方程为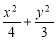 =1 4分
=1 4分
(2)设M(4,m),N(4,n),∵F1(-1,0),F2(1,0)
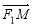 =(5,m),
=(5,m),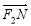 =(3,n),由
=(3,n),由 =0
=0 mn=-15<0 6分
mn=-15<0 6分
∴|MN|=|m-n|=|m|+|n|=|m|+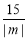 ≥2
≥2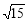 ∴|MN|的最小值为2
∴|MN|的最小值为2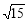 10分
10分
(3)以MN为直径的圆C的方程为:(x-4)2+(y-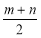 )=(
)=(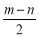 )2 11分
)2 11分
令y=0得(x-4)2=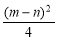 -
-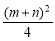 =-mn=15
=-mn=15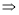 x=4±
x=4±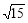
所以圆C过定点(4-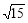 ,0)和(4+
,0)和(4+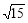 ,0) 13分
,0) 13分
考点:1.圆与圆锥曲线的综合;2.椭圆的简单性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目