题目内容
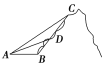
【题目】如图在△ABC中,已知点D在BC边上,满足AD⊥AC,cos ∠BAC=-![]() ,AB=3
,AB=3![]() ,BD=
,BD=![]() .
.
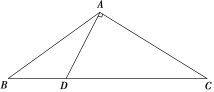
(1)求AD的长;
(2)求△ABC的面积.
【答案】见解析
【解析】(1)因为AD⊥AC,cos ∠BAC=-![]() ,
,
所以sin ∠BAC=![]() .
.
又sin ∠BAC=sin![]() =cos ∠BAD=
=cos ∠BAD=![]() ,
,
在△ABD中,BD2=AB2+AD2-2AB·AD·cos ∠BAD,
即AD2-8AD+15=0,
解得AD=5或AD=3,由于AB>AD,
所以AD=3.
(2)在△ABD中,![]() =
=![]() ,
,
又由cos ∠BAD=![]() 得sin ∠BAD=
得sin ∠BAD=![]() ,所以sin ∠ADB=
,所以sin ∠ADB=![]() ,则sin ∠ADC=sin(π-∠ADB)=sin ∠ADB=
,则sin ∠ADC=sin(π-∠ADB)=sin ∠ADB=![]() .
.
因为∠ADB=∠DAC+∠C=![]() +∠C,所以cos ∠C=
+∠C,所以cos ∠C=![]() .
.
在Rt△ADC中,cos ∠C=![]() ,则tan ∠C=
,则tan ∠C=![]() =
=![]() =
=![]() ,
,
所以AC=3![]() ,
,
则△ABC的面积S=![]() AB·AC·sin ∠BAC=
AB·AC·sin ∠BAC=![]() ×3
×3![]() ×3
×3![]() ×
×![]() =6
=6![]() .
.

【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远 (单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳 (单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a-1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则( )
A. 2号学生进入30秒跳绳决赛 B. 5号学生进入30秒跳绳决赛
C. 8号学生进入30秒跳绳决赛 D. 9号学生进入30秒跳绳决赛
【题目】下列四个命题中错误的是( )
A. 在一次试卷分析中,从每个考室中抽取第5号考生的成绩进行统计,不是简单随机抽样
B. 对一个样本容量为100的数据分组,各组的频数如下:
区间 |
|
|
|
|
|
|
|
|
频数 | 1 | 1 | 3 | 3 | 18 | 16 | 28 | 30 |
估计小于29的数据大约占总体的![]()
C. 设产品产量与产品质量之间的线性相关系数为![]() ,这说明二者存在着高度相关
,这说明二者存在着高度相关
D. 通过随机询问110名性别不同的行人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如表列联表.

由![]() ,则有
,则有![]() 以上的把握认为“选择过马路方式与性别有关”
以上的把握认为“选择过马路方式与性别有关”