��Ŀ����
��֪����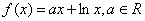 ��
��
��I������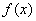 �ļ�ֵ��
�ļ�ֵ��
��II�����������ϵIJ�ͬ����P1��x1,y1����P2��x2,y2����������������ϵĵ�Q��x0,y0���� ��x1<x0<x2��ʹ�������ڵ�Q��������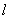 //P1P2,�����
//P1P2,�����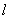 Ϊ��P1P2,�İ������ߡ�
Ϊ��P1P2,�İ������ߡ�
�ر�أ���x0 = 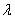 x1 + (1-
x1 + (1-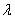 )x2
(0<
)x2
(0<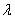 <1)ʱ���ֳ�
<1)ʱ���ֳ�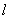 Ϊ��P1P2,��
Ϊ��P1P2,��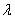 -�������ߡ�
-�������ߡ�
��i����֤������y=f(x)������һ���Ҿ��а������ߣ����Ұ���������Ψһ�ģ�
��ii���Ƿ��������C��ʹ������C������һ���Ҿ���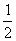 -�������ߣ������ڣ�����һ�����������ߣ���֤����Ľ��ۣ��������ڣ�˵�����ɡ�
-�������ߣ������ڣ�����һ�����������ߣ���֤����Ľ��ۣ��������ڣ�˵�����ɡ�
�⣺��I��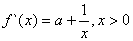
��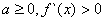 ������
������ ��
��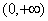 ������������
������������ ����
���� û�м�ֵ������3��
û�м�ֵ������3��
��a<0ʱ����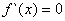 ����
����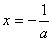 ��
��
��x�仯ʱ��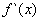 ��
�� �仯������±���
�仯������±���
|
x |
|
|
|
|
f`(x) |
+ |
0 |
- |
|
f(x) |
�������� |
����ֵ |
�����ݼ� |
 ��
��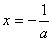 ʱ��f(x)ȡ�����ֵf(
ʱ��f(x)ȡ�����ֵf(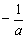 )=-1+ln(
)=-1+ln(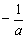 )�����ϣ���
)�����ϣ��� ʱ��f(x)û�м�ֵ��
ʱ��f(x)û�м�ֵ��
��a<0ʱ��f(x)�ļ���ֵΪ-1+ln(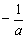 )��û�м�Сֵ��������������������������5��
)��û�м�Сֵ��������������������������5��
��II����i����P1(x1,f(x1)),P2(x2,f(x2))������y=f(x)�ϵ��������㣬Ҫ֤����P1P2�а������ߣ�ֻ��֤�����ڵ�Q(x0,f(x0))��x1<x0<x2��ʹ��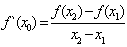 ��
��
�ҵ�Q����P1P2�ϡ���������������������������������������������������������7��
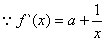 ����֤����
����֤���� ��ʹ��
��ʹ��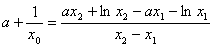 ����
����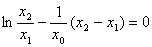 �������ҵ�Q����P1P2�ϡ�
�������ҵ�Q����P1P2�ϡ�
����֤������ �ڣ�x1,x2�����н⡣
�ڣ�x1,x2�����н⡣
��F(x)=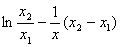 ����F(x)=
����F(x)=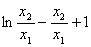 ����g(t) = lnt - t + 1��t>1��
����g(t) = lnt - t + 1��t>1��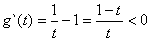 ��
�� g(t)��
g(t)��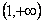 ���Ǽ�������
���Ǽ������� g(t)
<g(1)=0��ȡ
g(t)
<g(1)=0��ȡ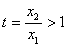 ����
����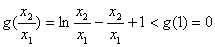 ����F(x1)<0��������������������������������9��
����F(x1)<0��������������������������������9��
ͬ����֤F(x2)>0,  F(x1)F(x2)<0��
F(x1)F(x2)<0�� ����F(x)=
����F(x)=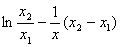 �ڣ�x1,x2��������㡣
�ڣ�x1,x2��������㡣
������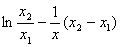 =0�ڣ�x1,x2�����н�x=x0����������������������10��
=0�ڣ�x1,x2�����н�x=x0����������������������10��
�ֶ��ں���g(t)= lnt - t + 1��ȡt= ����
���� ��
��
��֪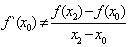 ������Q��P1P2�ϡ�F(x)����������
������Q��P1P2�ϡ�F(x)���������� F(x)�������Ψһ�ģ�
F(x)�������Ψһ�ģ�
������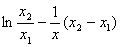 =0�ڣ�x1,x2������Ψһ�⡣
=0�ڣ�x1,x2������Ψһ�⡣
���ϣ�����y=f(x)������һ���Ҿ��а������ߣ����Ұ���������Ψһ�ġ�����������11��
��ii��ȡ����C��y=h(x)=x2��������y=h(x)������һ���Ҿ��� -�������ߡ�
-�������ߡ�
֤�����£�
��R��x3,y3��,S(x4,y4)������C���������㣨x3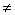 y4����
y4����
��
��
������C��y=x2������һ���Ҿ��� -�������ߡ�����������������������������14��
-�������ߡ�����������������������������14��

 �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д� ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
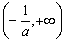
 ��
�� �������ABC�������
�������ABC������� ��
�� ��
�� ��
�� �ɵȲ����У���
�ɵȲ����У��� =9����a��ֵ��
=9����a��ֵ�� ��
�� ��ֵ��
��ֵ��