题目内容
 如图,设圆x2+y2=12与抛物线x2=4y相交于A,B两点,F为抛物线的焦点.
如图,设圆x2+y2=12与抛物线x2=4y相交于A,B两点,F为抛物线的焦点.(I)若过点F且斜率为1的直线l与抛物线和圆交于四个不同的点,从左至右依次为P1,P2,P3,P4,求|P1P2|+|P3+P4|的值;
(II)若直线m与抛物线相交于M,N两点,且与圆相切,切点D在劣弧
 | AB |
分析:(I)由圆的方程和抛物线的方程联解,求得交点A、B的坐标,从而判断直线l与圆交于P1、P3,直线l与抛物线交于P2、P4,
另|P1P2|+|P3+P4|的表达式用P1,P2,P3,P4的四点的横坐标表示,然后根据根与系数的关系,代入表达式,即解.
(II)先设直线m的方程y=k+b,交点M、N坐标,再用点M、N纵坐标表示出|MF|+|NF|,由与圆相切,得到k与b的关系,
消去k用b表示|MF|+|NF|,即得到关于b的一个函数,由kOA=-
,kOB=
,得到k的范围,由此求得b的范围,
再将b的代入|MF|+|NF|的函数关系式中并求出其范围.
另|P1P2|+|P3+P4|的表达式用P1,P2,P3,P4的四点的横坐标表示,然后根据根与系数的关系,代入表达式,即解.
(II)先设直线m的方程y=k+b,交点M、N坐标,再用点M、N纵坐标表示出|MF|+|NF|,由与圆相切,得到k与b的关系,
消去k用b表示|MF|+|NF|,即得到关于b的一个函数,由kOA=-
| ||
| 2 |
| ||
| 2 |
再将b的代入|MF|+|NF|的函数关系式中并求出其范围.
解答:解:(1)由
,得
或
,
即A(-2
,2),B(2
,2).
∵点F坐标为(0,1),∴kFB-
=
,所以kl>kFB,
所以直线l与圆交于P1、P3两点,与抛物线交于P2、P4两点,
设P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4)
把直线l方程:y=x+1代入x2=4y,得x2-4x-4=0,∴x2+x4=4;
把直线l方程:y=x+1代入x2+y2=12,得2x2+2x-11=0,∴x1+x3=-1
∴|P1P2|=
•|x1-x2|=
(x2-x1)
∴|P3P4|=
•|x3-x4|=
(x4-x3)
∴|P1P2|+|P3P4|=
[(x2-x1)+(x4-x3)]=
[(x2+x4)-(x1+x3)]
=
[4-(-1)]=5
.
所以|P1P2|+|P3+P4|的值等于5
.
(II)设直线m的方程为y=k+b(b>0),
代入抛物线方程得x2-4kx-4b=0,
设点M(x1,y1),N(x2,y2),则x1+x2=4k,
则y1+y2=k(x1+x2)+2b=4k2+2b,
∵直线m与该圆相切,∴
=
即 k2=
-1,
又|MF|=y1+1,|NF|=y2+1,
∴|MF|+|NF|=y1+y2+2=4k2+2b+2=
+2b-2=
(b+3)2 -5
∵kOA=-
,kOB=
,∴分别过A、B的圆的切线的斜率为
,-
.
∴k∈[-
,
]∴0≤k2≤2,∴0≤
-1≤12,又b>0,∴b∈[2
,6]
所以|MF|+|NF|的取值范围为[2+4
,22].
|
|
|
即A(-2
| 2 |
| 2 |
∵点F坐标为(0,1),∴kFB-
| 1 | ||
2
|
| ||
| 4 |
所以直线l与圆交于P1、P3两点,与抛物线交于P2、P4两点,
设P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4)
把直线l方程:y=x+1代入x2=4y,得x2-4x-4=0,∴x2+x4=4;
把直线l方程:y=x+1代入x2+y2=12,得2x2+2x-11=0,∴x1+x3=-1
∴|P1P2|=
| 1+k2 |
| 2 |
∴|P3P4|=
| 1+k2 |
| 2 |
∴|P1P2|+|P3P4|=
| 2 |
| 2 |
=
| 2 |
| 2 |
所以|P1P2|+|P3+P4|的值等于5
| 2 |
(II)设直线m的方程为y=k+b(b>0),
代入抛物线方程得x2-4kx-4b=0,
设点M(x1,y1),N(x2,y2),则x1+x2=4k,
则y1+y2=k(x1+x2)+2b=4k2+2b,
∵直线m与该圆相切,∴
| b | ||
|
| 12 |
| b2 |
| 12 |
又|MF|=y1+1,|NF|=y2+1,
∴|MF|+|NF|=y1+y2+2=4k2+2b+2=
| b2 |
| 3 |
| 1 |
| 3 |
∵kOA=-
| ||
| 2 |
| ||
| 2 |
| 2 |
| 2 |
∴k∈[-
| 2 |
| 2 |
| b2 |
| 12 |
| 3 |
所以|MF|+|NF|的取值范围为[2+4
| 3 |
点评:此题考查用坐标法解决圆锥曲线问题,在解题过程中还考查了弦长公式的运用,同时还考查学生的计算技巧中设而不求的方法.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
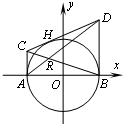 如图,过圆x2+y2=4与x的两个交点A、B,作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD于C、D两点,设AD、BC的交点为R.
如图,过圆x2+y2=4与x的两个交点A、B,作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD于C、D两点,设AD、BC的交点为R. (2011•临沂二模)如图,过圆x2+y2=4与x轴的两个交点A、B作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD与C、D两点,设AD、BC的交点为R.
(2011•临沂二模)如图,过圆x2+y2=4与x轴的两个交点A、B作圆的切线AC、BD,再过圆上任意一点H作圆的切线,交AC、BD与C、D两点,设AD、BC的交点为R.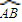 上,求|MF|+|NF|的取值范围.
上,求|MF|+|NF|的取值范围.
 上,求|MF|+|NF|的取值范围.
上,求|MF|+|NF|的取值范围.