题目内容
已知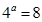 ,
,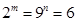 ,且
,且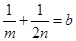 ,则
,则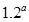 与
与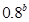 的大小关系_______.
的大小关系_______.
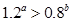
解析试题分析:由 ,又由
,又由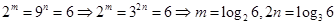 ,所以
,所以 ,所以由
,所以由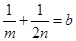 可得
可得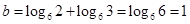 ,所以
,所以 ,
, ,所以
,所以 即
即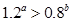 .
.
考点:1.分数指数幂的运算;2.对数的运算;3.指数函数的单调性.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
题目内容
已知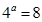 ,
,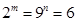 ,且
,且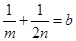 ,则
,则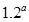 与
与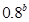 的大小关系_______.
的大小关系_______.
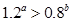
解析试题分析:由 ,又由
,又由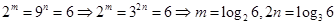 ,所以
,所以 ,所以由
,所以由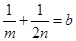 可得
可得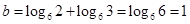 ,所以
,所以 ,
, ,所以
,所以 即
即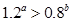 .
.
考点:1.分数指数幂的运算;2.对数的运算;3.指数函数的单调性.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案