题目内容
17.已知圆(x+1)2+y2=4的圆心为C,点P是直线l:mx-y-5m+4=0上的点,若该圆上存在点Q使得∠CPQ=30°,则实数m的取值范围为( )| A. | [-1,1] | B. | [-2,2] | C. | $[{\frac{{\sqrt{3}-3}}{4},\frac{{\sqrt{3}+3}}{4}}]$ | D. | $[{0,\frac{12}{5}}]$ |
分析 由题意,从直线上的点向圆上的点连线成角,当且仅当两条线均为切线时才是最大的角,此时CP=4,利用圆上存在点Q使得∠CPQ=30°,可得圆心到直线的距离d=$\frac{|-6m+4|}{\sqrt{{m}^{2}+1}}$≤4,进而得出答案.
解答 解:由题意,从直线上的点向圆上的点连线成角,当且仅当两条线均为切线时才是最大的角,此时CP=4.
∵圆上存在点Q使得∠CPQ=30°,
∴圆心到直线的距离d=$\frac{|-6m+4|}{\sqrt{{m}^{2}+1}}$≤4,
∴0≤m≤$\frac{12}{5}$,
故选:D.
点评 本题考查了直线与圆相切的性质、点到直线的距离的计算公式、数形结合思想方法,属于中档题.

练习册系列答案
相关题目
9.已知函数f(x)=sin(ωx+$\frac{π}{3}$)+$\sqrt{3}$sin(ωx-$\frac{π}{6}$)(ω>0,x∈R)的最小正周期为π,则( )
| A. | f(x)为偶函数 | B. | f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上单调递增 | ||
| C. | x=$\frac{π}{2}$为f(x)的图象的一条对称轴 | D. | ($\frac{π}{2}$,0)为f(x)的图象的一个对称中心 |
6.若x,y满足$\left\{\begin{array}{l}x+y≥0\\ x≥1\\ x-y≥0\end{array}\right.$,则下列不等式恒成立的是( )
| A. | y≥-1 | B. | x≥2 | C. | x+2y+2≥0 | D. | 2x-y+1≥0 |
12.已知不共线向量$\overrightarrow{a}$,$\overrightarrow{b}$,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$的夹角是( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
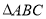 中,内角
中,内角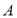 ,
,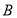 ,
,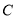 的对边分别为
的对边分别为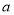 ,
,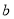 ,
,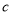 ,且
,且 ,已知
,已知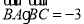 ,
,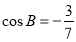 ,
, .求:
.求: 和
和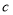 的值;
的值;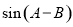 的值.
的值.