题目内容
 (2013•杭州二模)如图,已知在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA=
(2013•杭州二模)如图,已知在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,PA=| 3 |
(Ⅰ)求证:PH∥平面GED;
(Ⅱ)过点F作平面α,使ED∥平面α,当平面α⊥平面EDG时,设PA与平面α交于点Q,求PQ的长.
分析:(I)连接HC,交ED于点N,连接GN.由平行四边形的性质和三角形的中位线定理即可得到GN∥PH,再利用线面平行的判定定理即可证明;
(II)方法一:通过建立空间直角坐标系,利用平面GED⊥平面α?两个平面的法向量
•
=0,求得Q的坐标,进而取得|PQ|的长.
方法二:连接BH,则BH∥ED,及PB∥GE,可得平面PBH∥平面GED;利用三角形懂得中位线定理可得FM∥BK;利用菱形的性质可得AE⊥BK,再利用线面垂直的判定和性质定理可得BK⊥平面PAK,FM⊥平面PAK;过M作MQ⊥PK,交PA于Q,设MQ与FM所确定的平面为α,可得ED∥BH∥FM,ED∥平面α,又平面α⊥平面PBH,可得平面α⊥平面EDG.得平面α满足条件.利用已知可得PA、AK、PK,再利用
=
,即可得到PQ.
(II)方法一:通过建立空间直角坐标系,利用平面GED⊥平面α?两个平面的法向量
| n1 |
| n2 |
方法二:连接BH,则BH∥ED,及PB∥GE,可得平面PBH∥平面GED;利用三角形懂得中位线定理可得FM∥BK;利用菱形的性质可得AE⊥BK,再利用线面垂直的判定和性质定理可得BK⊥平面PAK,FM⊥平面PAK;过M作MQ⊥PK,交PA于Q,设MQ与FM所确定的平面为α,可得ED∥BH∥FM,ED∥平面α,又平面α⊥平面PBH,可得平面α⊥平面EDG.得平面α满足条件.利用已知可得PA、AK、PK,再利用
| PQ |
| PK |
| PM |
| PA |
解答:(Ⅰ)证明:连接HC,交ED于点N,连接GN,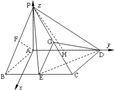
∵DHEC是平行四边形,∴N是线段HC的中点,又G是PC的中点,
∴GN∥PH,
又∵GN?平面GED,PH?平面GED,
∴PH∥平面GED.
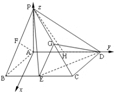
(Ⅱ) 方法1:连接AE,∵∠BAD=120°,∴△ABE是等边三角形,
设BE的中点为M,以AM、AD、AP分别为x,y,z轴建立空间直角坐标系.
则B(
,-
,0),C(
,
,0),D(0,2,0),P(0,0,
),
则E(
,
,0),F(
,-
,
),G(
,
,
).
设Q(0,0,t),
=(-
,
,0),
=(
,-
,
).
设
=(x1,y1,z1)是平面GED的一个法向量,
则
,得
,
令y1=1∴
=(
,1,
).
设
=(x2,y2,z2)是平面α的一个法向量,
则
,得
,令y2=1,得
=(
,1,
),
当平面GED⊥平面α时,
•
=3+1+
•
=0,
得t=
=
,则PQ的长为
-
=
.
方法2:连接BH,则BH∥ED,又∵PB∥GE,∴平面PBH∥平面GED,
设BH与AE交于点K,PK的中点为M,
∵F是PB的中点,∴FM∥BK,
∵ABEH是菱形,∴AE⊥BK,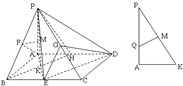
∵PA⊥平面ABCD,∴PA⊥BK,∴BK⊥平面PAK.
∴FM⊥平面PAK,
过M作MQ⊥PK,交PA于Q,设MQ与FM所确定的平面为α,
∵ED∥BH∥FM,∴ED∥平面α,又平面α⊥平面PBH,∴平面α⊥平面EDG.
得平面α满足条件.
∵PA=
,AK=
,∴PK=
=
,
由
=
,
得PQ=
=
=
.

∵DHEC是平行四边形,∴N是线段HC的中点,又G是PC的中点,
∴GN∥PH,
又∵GN?平面GED,PH?平面GED,
∴PH∥平面GED.
(Ⅱ) 方法1:连接AE,∵∠BAD=120°,∴△ABE是等边三角形,
设BE的中点为M,以AM、AD、AP分别为x,y,z轴建立空间直角坐标系.
则B(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
则E(
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| 1 |
| 4 |
| ||
| 2 |
| ||
| 4 |
| 3 |
| 4 |
| ||
| 2 |
设Q(0,0,t),
| ED |
| ||
| 2 |
| 3 |
| 2 |
| DG |
| ||
| 4 |
| 5 |
| 4 |
| ||
| 2 |
设
| n1 |
则
|
|

令y1=1∴
| n1 |
| 3 |
| ||
| 3 |
设
| n2 |
则
|
|
| n2 |
| 3 |
| 1 | ||
2t-
|
当平面GED⊥平面α时,
| n1 |
| n2 |
| ||
| 3 |
| 1 | ||
2t-
|
得t=
| 11 | ||
8
|
11
| ||
| 24 |
| 3 |
11
| ||
| 24 |
13
| ||
| 24 |
方法2:连接BH,则BH∥ED,又∵PB∥GE,∴平面PBH∥平面GED,
设BH与AE交于点K,PK的中点为M,
∵F是PB的中点,∴FM∥BK,
∵ABEH是菱形,∴AE⊥BK,

∵PA⊥平面ABCD,∴PA⊥BK,∴BK⊥平面PAK.
∴FM⊥平面PAK,
过M作MQ⊥PK,交PA于Q,设MQ与FM所确定的平面为α,
∵ED∥BH∥FM,∴ED∥平面α,又平面α⊥平面PBH,∴平面α⊥平面EDG.
得平面α满足条件.
∵PA=
| 3 |
| 1 |
| 2 |
3+
|
| ||
| 2 |
由
| PQ |
| PK |
| PM |
| PA |
得PQ=
| PK•PM |
| PA |
| ||||||||
|
13
| ||
| 24 |
点评:本题综合考查了线面平行于垂直、面面平行与垂直、建立空间直角坐标系得出二面角的法向量、平行四边形的性质、三角形的中位线定理等基础知识与基本技能,考查了空间想象能力、推理能力与计算能力.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目