题目内容
已知二次函数y=f(x)在x=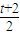 处取得最小值-
处取得最小值-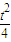 (t>0),f(1)=0
(t>0),f(1)=0(1)求y=f(x)的表达式;
(2)若任意实数x都满足f(x)•g(x)+anx+bn=xn+1(g(x)为多项式,n∈N+),试用t表示an和bn;
(3)设圆Cn的方程(x-an)2+(y-bn)2=rn2,圆Cn与Cn+1外切(n=1,2,3,…),{rn}是各项都是正数的等比数列,记Sn为前n个圆的面积之和,求rn,Sn.
【答案】分析:(1)根据条件可设二次函数的顶点式f(x)=a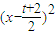 --
--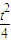 ,由f(1)=0,可得a,从而有f(x)=x2-(t+2)x+(t+1).
,由f(1)=0,可得a,从而有f(x)=x2-(t+2)x+(t+1).
(2)由f(x)=x2-(t+2)x+(t+1)=(x-1)(x-t-1),所以“f(x)•g(x)+anx+bn=xn+1”转化为:(x-1)(x-t-1)g(x)+anx+bn=xn+1.要消去g(x)将x=1,x=t+1别代入上式,得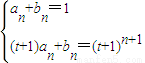 ,解方程组即可.
,解方程组即可.
(3)由an+bn=1,可知圆Cn的圆心On在直线x+y=1上,可求得圆心距|OnOn+1|=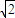 |an+1-an|=
|an+1-an|=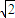 (t+1)n+1再由圆Cn与Cn+1外切,可得rn+rn+1=
(t+1)n+1再由圆Cn与Cn+1外切,可得rn+rn+1=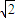 (t+1)n+1设{rn}的公比为q,有
(t+1)n+1设{rn}的公比为q,有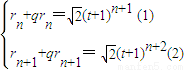 得q=
得q=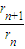 =t+1从而求得通项及前n项和
=t+1从而求得通项及前n项和
解答:解:(1)设f(x)=a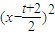 --
--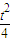 ,
,
∵f(1)=0,
∴a --
--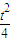 =0,从而a=1,
=0,从而a=1,
∴f(x)=x2-(t+2)x+(t+1).
(2)f(x)=x2-(t+2)x+(t+1)=(x-1)(x-t-1)
∴(x-1)(x-t-1)g(x)+anx+bn=xn+1.
将x=1,x=t+(1分)别代入上式,得

∵t≠0,
∴an= [(t+1)n+1-1]
[(t+1)n+1-1]
bn=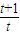 [1-(t+1)n]
[1-(t+1)n]
(3)∵an+bn=1,
∴圆Cn的圆心On在直线x+y=1上
∴|OnOn+1|=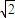 |an+1-an|=
|an+1-an|=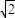 (t+1)n+1
(t+1)n+1
又圆Cn与Cn+1外切,故rn+rn+1=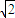 (t+1)n+1
(t+1)n+1
设{rn}的公比为q,则
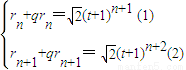
(2)÷(1),得q=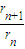 =t+1
=t+1
于是rn=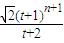 ∴Sn=π(r12+r22+…+rn2)=
∴Sn=π(r12+r22+…+rn2)= =
=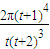 [(t+1)2n-1]
[(t+1)2n-1]
点评:本题主要考查数列与函数,方程的综合运用,主要涉及了函数的解析式,圆与圆的位置关系,数列的递推与通项和前n项和公式.
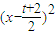 --
--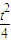 ,由f(1)=0,可得a,从而有f(x)=x2-(t+2)x+(t+1).
,由f(1)=0,可得a,从而有f(x)=x2-(t+2)x+(t+1).(2)由f(x)=x2-(t+2)x+(t+1)=(x-1)(x-t-1),所以“f(x)•g(x)+anx+bn=xn+1”转化为:(x-1)(x-t-1)g(x)+anx+bn=xn+1.要消去g(x)将x=1,x=t+1别代入上式,得
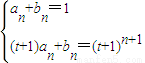 ,解方程组即可.
,解方程组即可.(3)由an+bn=1,可知圆Cn的圆心On在直线x+y=1上,可求得圆心距|OnOn+1|=
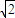 |an+1-an|=
|an+1-an|=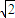 (t+1)n+1再由圆Cn与Cn+1外切,可得rn+rn+1=
(t+1)n+1再由圆Cn与Cn+1外切,可得rn+rn+1=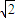 (t+1)n+1设{rn}的公比为q,有
(t+1)n+1设{rn}的公比为q,有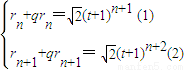 得q=
得q=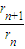 =t+1从而求得通项及前n项和
=t+1从而求得通项及前n项和解答:解:(1)设f(x)=a
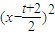 --
--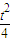 ,
,∵f(1)=0,
∴a
 --
--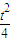 =0,从而a=1,
=0,从而a=1,∴f(x)=x2-(t+2)x+(t+1).
(2)f(x)=x2-(t+2)x+(t+1)=(x-1)(x-t-1)
∴(x-1)(x-t-1)g(x)+anx+bn=xn+1.
将x=1,x=t+(1分)别代入上式,得

∵t≠0,
∴an=
 [(t+1)n+1-1]
[(t+1)n+1-1]bn=
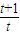 [1-(t+1)n]
[1-(t+1)n](3)∵an+bn=1,
∴圆Cn的圆心On在直线x+y=1上
∴|OnOn+1|=
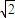 |an+1-an|=
|an+1-an|=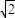 (t+1)n+1
(t+1)n+1又圆Cn与Cn+1外切,故rn+rn+1=
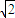 (t+1)n+1
(t+1)n+1设{rn}的公比为q,则
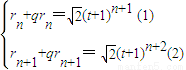
(2)÷(1),得q=
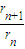 =t+1
=t+1于是rn=
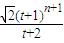 ∴Sn=π(r12+r22+…+rn2)=
∴Sn=π(r12+r22+…+rn2)= =
=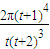 [(t+1)2n-1]
[(t+1)2n-1]点评:本题主要考查数列与函数,方程的综合运用,主要涉及了函数的解析式,圆与圆的位置关系,数列的递推与通项和前n项和公式.

练习册系列答案
相关题目
 已知二次函数y=f(x)的图象如图所示:
已知二次函数y=f(x)的图象如图所示: