题目内容
已知二次函数y=f(x)=x2+bx+c的图象过点(1,13),且函数y=f(x-
)是偶函数.
(1)求f(x)的解析式;
(2)已知t<2,g(x)=[f(x)-x2-13]•|x|,求函数g(x)在[t,2]上的最大值和最小值;
(3)函数y=f(x)的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
| 1 | 2 |
(1)求f(x)的解析式;
(2)已知t<2,g(x)=[f(x)-x2-13]•|x|,求函数g(x)在[t,2]上的最大值和最小值;
(3)函数y=f(x)的图象上是否存在这样的点,其横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
分析:(1)因为函数y=f(x-
)是偶函数,所以二次函数f(x)=x2+bx+c的对称轴方程为x=-
,由此求得b的值,再由
f(x)=x2+bx+c的图象过点(1,13),求出c的值,从而求得f(x)的解析式.
(2)由题意可得 g(x)=(x-2)•|x|,画出它的图象,讨论t的范围,结合图象求出g(x)在[t,2]上的 最值.
(3)如果函数y=f(x)的图象上存在符合要求的点,设为P(m,n2),从而4n2-(2m+1)2=43,由此求得m、n的值,
从而得出结论.
| 1 |
| 2 |
| 1 |
| 2 |
f(x)=x2+bx+c的图象过点(1,13),求出c的值,从而求得f(x)的解析式.
(2)由题意可得 g(x)=(x-2)•|x|,画出它的图象,讨论t的范围,结合图象求出g(x)在[t,2]上的 最值.
(3)如果函数y=f(x)的图象上存在符合要求的点,设为P(m,n2),从而4n2-(2m+1)2=43,由此求得m、n的值,
从而得出结论.
解答:解:(1)因为函数y=f(x-
)是偶函数,所以二次函数f(x)=x2+bx+c的对称轴方程为x=-
,故b=1.--(2分)
又因为二次函数f(x)=x2+bx+c的图象过点(1,13),所以1+b+c=13,故c=11.
因此,f(x)的解析式为f(x)=x2+x+11.-----(4分)
(2)由题意可得 g(x)=(x-2)•|x|,当x≤0时,g(x)=-(x-1)2+1,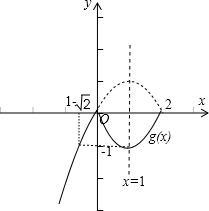
当x>0时,g(x)=(x-1)2-1,由此可知g(x)在[t,2]上的最大值 g(x)max=g(2)=0.----(7分)
当1≤t<2,g(x)min =g(t)=t2-2t.
当1-
≤t<1,g(x)min=g(1)=-1.
当t<1-
,g(x)min=g(t)=-t2+2t.---(10分)
(3)如果函数y=f(x)的图象上存在符合要求的点,设为P(m,n2),
其中m为正整数,n为自然数,则m2+m+11=n2,从而4n2-(2m+1)2=43,
即[2n+(2m+1)][2n-(2m+1)]=43.-----(12分)
注意到43是质数,且2n+(2m+1)>2n-(2m+1),2n+(2m+1)>0,
所以有
,解得
.----(15分)
因此,函数y=f(x)的图象上存在符合要求的点,它的坐标为(10,121).-------(16分)
| 1 |
| 2 |
| 1 |
| 2 |
又因为二次函数f(x)=x2+bx+c的图象过点(1,13),所以1+b+c=13,故c=11.
因此,f(x)的解析式为f(x)=x2+x+11.-----(4分)
(2)由题意可得 g(x)=(x-2)•|x|,当x≤0时,g(x)=-(x-1)2+1,

当x>0时,g(x)=(x-1)2-1,由此可知g(x)在[t,2]上的最大值 g(x)max=g(2)=0.----(7分)
当1≤t<2,g(x)min =g(t)=t2-2t.
当1-
| 2 |
当t<1-
| 2 |
(3)如果函数y=f(x)的图象上存在符合要求的点,设为P(m,n2),
其中m为正整数,n为自然数,则m2+m+11=n2,从而4n2-(2m+1)2=43,
即[2n+(2m+1)][2n-(2m+1)]=43.-----(12分)
注意到43是质数,且2n+(2m+1)>2n-(2m+1),2n+(2m+1)>0,
所以有
|
|
因此,函数y=f(x)的图象上存在符合要求的点,它的坐标为(10,121).-------(16分)
点评:本题主要考查二次函数的性质应用,求二次函数在闭区间上的最值的方法,体现了分类讨论、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
 已知二次函数y=f(x)的图象如图所示:
已知二次函数y=f(x)的图象如图所示: