��Ŀ����
����Ŀ��ij��ѧ���ڼ�ֹ᳹����Ϊ�������ʩ�̵Ľ������ÿ�궼����У�Ļ����ڼ���С���ѧ�����������ԡ��͡����������������ԡ�������ԣ��Ը�ѧ��������Ȥѧϰ�������ṩ�ο����ݣ��ɼ���Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����ȼ����ȼ�
����ȼ����ȼ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ��Ӧ5�֣�4�֣�3�֣�2�֣�1�֣���ij��ѧ�����ƵĿ��Գɼ�������ͳ����ͼ��ʾ�����С����������������ԡ���Ŀ�ijɼ�Ϊ
�ֱ��Ӧ5�֣�4�֣�3�֣�2�֣�1�֣���ij��ѧ�����ƵĿ��Գɼ�������ͳ����ͼ��ʾ�����С����������������ԡ���Ŀ�ijɼ�Ϊ![]() �Ŀ�����3�ˣ�
�Ŀ�����3�ˣ�
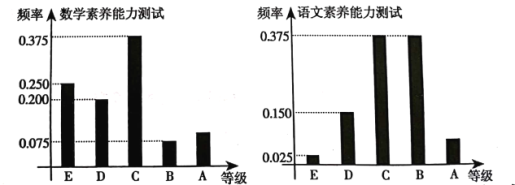
��1����ðࡰ��ѧ�����������ԡ��Ŀ�Ŀƽ�����Լ�����ѧ�����������ԡ���Ŀ�ɼ�Ϊ![]() ��������
��������
��2�����ð��9�˵÷ִ���7�֣�������2��10�֣�3��9�֣�4��8�֣�����9���������ȡ���ˣ������˵ijɼ�֮��Ϊ![]() ����
����![]() ��
��
��3���Ӹð�÷ִ���7�ֵ�9����ѡ3�˼��ף��ң�����Ӳμ�ѧУ�ڵġ���ѧ��ʱ������ս����������Ϊ��ÿ��������һ����Ա�μ���ս����������ʱ�䣬������������⣬���Ŷ���ս�ɹ���������ս�����������ʧ�ܣ���������һ����Ա��ȥ��ս��ֱ�������ԱΪֹ��ͨ��ѵ������֪�ף��ң���ͨ����ս���ĸ��ʷֱ���![]() ��
��![]() ��
��![]() �������������Ⱥ�˳���ɳ���Ա����ʹ���ɳ���Ա��Ŀ�ľ�ֵ�ﵽ��С����ֻ��д�������
�������������Ⱥ�˳���ɳ���Ա����ʹ���ɳ���Ա��Ŀ�ľ�ֵ�ﵽ��С����ֻ��д�������
���𰸡���1��2.575,4����2��![]() ����3���ң��ף�����
����3���ң��ף�����
��������
��1������Ƶ�ʷֲ�ֱ��ͼ��ֱ�����Ȩƽ�������ٸ�������������������Ϊ![]() ��Ƶ�ʺ������ó����������ٸ��ݡ���ѧ�����������ԡ���Ŀ��Ƶ�ʼ��ɵý�.
��Ƶ�ʺ������ó����������ٸ��ݡ���ѧ�����������ԡ���Ŀ��Ƶ�ʼ��ɵý�.
��1����ͼ��֪����ѧ������������Ϊ![]() ��Ƶ��Ϊ0.1���ʸðࡰ��ѧ�����������ԡ��Ŀ�Ŀƽ����Ϊ
��Ƶ��Ϊ0.1���ʸðࡰ��ѧ�����������ԡ��Ŀ�Ŀƽ����Ϊ![]() ��
��
����������������Ϊ![]() ��Ƶ��Ϊ0.075���ʶ��ð���
��Ƶ��Ϊ0.075���ʶ��ð���![]() �ˣ�����ѧ�����������ԡ���Ŀ�ɼ�Ϊ
�ˣ�����ѧ�����������ԡ���Ŀ�ɼ�Ϊ![]() ������
������![]() ���ˣ���
���ˣ���
��2�����⣺![]() ��ȡֵ��Ϊ29��28��27��26��25��24��
��ȡֵ��Ϊ29��28��27��26��25��24��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]()
![]() ��
��
��3���ң��ף�����

����Ŀ����ȫ�濹���¹ڷ���������һ����ʱ�ڣ����н����������ͣ�β�ͣѧ���Ŀںţ�����ѧ������ѧϰ.ijУ��ѧ��ʦΪ�˵������ѧ����ѧ�ɼ�������ѧϰʱ��֮�����ع�ϵ���Ը����꼶���ѡȡ45��ѧ�����и����ʾ�������ÿ������ѧϰ��ѧʱ�䲻����5Сʱ����19�ˣ����µ����У��ڼ�⿼������ѧƽ���ɼ�����120�ֵ�ռ![]() ��ͳ�Ƴɼ���õ�����
��ͳ�Ƴɼ���õ�����![]() ��������
��������
����������120�� | ��������120�� | �ϼ� | |
����ѧϰʱ�䲻����5Сʱ | 4 | 19 | |
����ѧϰʱ�䲻��5Сʱ | |||
�ϼ� | 45 |
��1�����������![]() �����������ж��Ƿ���99%�İ�����Ϊ������ѧ������ѧ�ɼ���ѧ������ѧϰʱ���йء���
�����������ж��Ƿ���99%�İ�����Ϊ������ѧ������ѧ�ɼ���ѧ������ѧϰʱ���йء���
��2���ٰ��շֲ�����ķ����������������дӷ���������120�ֺͷ�������120�ֵ�����ѧ���г�ȡ9��ѧ������鵽����120����ÿ������ѧϰʱ�䲻��5Сʱ��������![]() ����
����![]() �ķֲ��У��������������ʽ��ʾ����
�ķֲ��У��������������ʽ��ʾ����
������Ƶ����Ϊ���ʣ���ȫУ�����ôμ����ѧ�ɼ�������120�ֵ�ѧ���������ȡ20�ˣ�����Щ����ÿ������ѧϰʱ�䲻����5Сʱ�������������ͷ���.
��������ٽ�ֵ�����ο���
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���ο���ʽ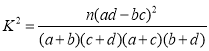 ����
����![]() ��
��