题目内容
若函数f(x)对定义域中任意x均满足f(x)+f(2a-x)=2b,则称函数y=f(x)的图象关于点(a,b)对称.(Ⅰ)已知函数
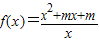 的图象关于点(0,1)对称,求实数m的值;
的图象关于点(0,1)对称,求实数m的值;(Ⅱ)已知函数g(x)在(-∞,0)∪(0,+∞)上的图象关于点(0,1)对称,且当x∈(0,+∞)时,g(x)=x2+ax+1,求函数g(x)在(-∞,0)上的解析式;
(Ⅲ)在(Ⅰ)、(Ⅱ)的条件下,当t>0时,若对任意实数x∈(-∞,0),恒有g(x)<f(t)成立,求实数a的取值范围.
【答案】分析:(Ⅰ)利用函数 的图象关于点(0,1)对称,可得f(x)+f(-x)=2,代入解析式,即可求得m的值;
的图象关于点(0,1)对称,可得f(x)+f(-x)=2,代入解析式,即可求得m的值;
(Ⅱ)利用函数g(x)在(-∞,0)∪(0,+∞)上的图象关于点(0,1)对称,可得g(x)+g(-x)=2,根据x∈(0,+∞)时的解析式,即可求得结论;
(Ⅲ)对任意实数x∈(-∞,0),恒有g(x)<f(t)成立,等价于g(x)max<f(t)min,由此可求实数a的取值范围.
解答:解:(Ⅰ)由题设,∵函数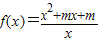 的图象关于点(0,1)对称,
的图象关于点(0,1)对称,
∴f(x)+f(-x)=2,
∴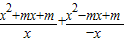 =2
=2
∴m=1…(4分)
(Ⅱ)∵函数g(x)在(-∞,0)∪(0,+∞)上的图象关于点(0,1)对称,
∴g(x)+g(-x)=2,
∵当x∈(0,+∞)时,g(x)=x2+ax+1,
∴当x<0时,g(x)=2-g(-x)=-x2+ax+1…(8分)
(Ⅲ)由(Ⅰ)得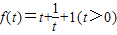 ,其最小值为f(1)=3
,其最小值为f(1)=3
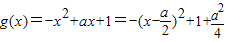 ,…(10分)
,…(10分)
①当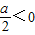 ,即a<0时,
,即a<0时,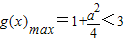 ,∴
,∴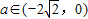 …(12分)
…(12分)
②当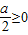 ,即a≥0时,g(x)max<1<3,∴a∈[0,+∞)…(13分)
,即a≥0时,g(x)max<1<3,∴a∈[0,+∞)…(13分)
由①、②得 …(14分)
…(14分)
点评:本题考查函数的对称性,考查函数的解析式,考查恒成立问题,正确求出函数的最值是关键.
 的图象关于点(0,1)对称,可得f(x)+f(-x)=2,代入解析式,即可求得m的值;
的图象关于点(0,1)对称,可得f(x)+f(-x)=2,代入解析式,即可求得m的值;(Ⅱ)利用函数g(x)在(-∞,0)∪(0,+∞)上的图象关于点(0,1)对称,可得g(x)+g(-x)=2,根据x∈(0,+∞)时的解析式,即可求得结论;
(Ⅲ)对任意实数x∈(-∞,0),恒有g(x)<f(t)成立,等价于g(x)max<f(t)min,由此可求实数a的取值范围.
解答:解:(Ⅰ)由题设,∵函数
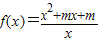 的图象关于点(0,1)对称,
的图象关于点(0,1)对称,∴f(x)+f(-x)=2,
∴
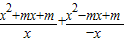 =2
=2∴m=1…(4分)
(Ⅱ)∵函数g(x)在(-∞,0)∪(0,+∞)上的图象关于点(0,1)对称,
∴g(x)+g(-x)=2,
∵当x∈(0,+∞)时,g(x)=x2+ax+1,
∴当x<0时,g(x)=2-g(-x)=-x2+ax+1…(8分)
(Ⅲ)由(Ⅰ)得
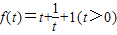 ,其最小值为f(1)=3
,其最小值为f(1)=3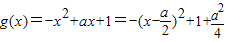 ,…(10分)
,…(10分)①当
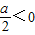 ,即a<0时,
,即a<0时,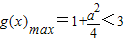 ,∴
,∴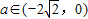 …(12分)
…(12分)②当
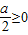 ,即a≥0时,g(x)max<1<3,∴a∈[0,+∞)…(13分)
,即a≥0时,g(x)max<1<3,∴a∈[0,+∞)…(13分)由①、②得
 …(14分)
…(14分)点评:本题考查函数的对称性,考查函数的解析式,考查恒成立问题,正确求出函数的最值是关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
 图象的对称中心是(1,1)
图象的对称中心是(1,1) ,则函数f(x)=
,则函数f(x)=
 对任意的x1≠x2都有
对任意的x1≠x2都有 ,则实数a的
,则实数a的 ]
]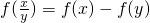 ,则不等式
,则不等式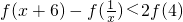 的解为
的解为