题目内容
自点A(-3,3)发出的光线l射到x轴上,被x轴反射,反射光线所在的直线与圆C:x2+y2-4x-4y+7=0相切.求:
(1)光线l和反射光线所在的直线方程;
(2)光线自A到切点所经过的路程.
(1)光线l和反射光线所在的直线方程;
(2)光线自A到切点所经过的路程.
(1)4x+3y+3=0或3x+4y-3=0.(2)7
根据对称关系,首先求出点A的对称点A′的坐标为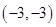 ,其次设过A′的圆C的切线方程为y=k
,其次设过A′的圆C的切线方程为y=k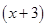 -3.
-3.
根据d=r,即求出圆C的切线的斜率为k=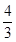 或k=
或k=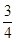 ,
,
进一步求出反射光线所在的直线的方程为
4x-3y+3=0或3x-4y-3=0.
最后根据入射光与反射光关于x轴对称,求出入射光所在直线方程为4x+3y+3=0或3x+4y-3=0.
光路的距离为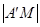 ,可由勾股定理求得
,可由勾股定理求得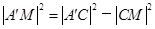 =7.
=7.
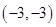 ,其次设过A′的圆C的切线方程为y=k
,其次设过A′的圆C的切线方程为y=k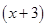 -3.
-3.根据d=r,即求出圆C的切线的斜率为k=
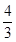 或k=
或k=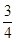 ,
,进一步求出反射光线所在的直线的方程为
4x-3y+3=0或3x-4y-3=0.
最后根据入射光与反射光关于x轴对称,求出入射光所在直线方程为4x+3y+3=0或3x+4y-3=0.
光路的距离为
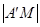 ,可由勾股定理求得
,可由勾股定理求得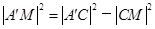 =7.
=7.
练习册系列答案
相关题目
 中,顶点
中,顶点 ,边
,边 上的中线
上的中线 所在直线的方程是
所在直线的方程是 ,边
,边 上高
上高 所在直线的方程是
所在直线的方程是 .
. 、C的坐标; (2)求
、C的坐标; (2)求 与
与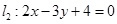 ,若
,若 的交点在
的交点在 轴上,则
轴上,则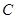 的值为( )
的值为( ) 的取值有关
的取值有关 中,若圆
中,若圆 上存在
上存在 ,
, 两点,且弦
两点,且弦 的中点为
的中点为 ,则直线
,则直线 的方程为 .
的方程为 . 
 ,求直线l的方程;
,求直线l的方程;