题目内容
若a>0,b>0,且a+b=1,则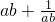 的最小值为
的最小值为
- A.

- B.

- C.

- D.2
B
分析:由a>0,b>0利用基本不等式可得,1=a+b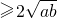 从而可得
从而可得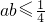 令t=ab则t∈(0,
令t=ab则t∈(0, ]
]
通过考查函数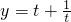 在(0,
在(0,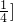 单调性可求函数的最小值
单调性可求函数的最小值
解答:∵a>0,b>0
利用基本不等式可得,1=a+b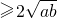 ∴
∴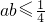
令t=ab则t∈(0, ]
]
而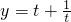 在(0,
在(0,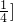 单调递减
单调递减
∴当t= 时函数有最小值
时函数有最小值
故选B
点评:本题主要考查了基本不等式 的应用,及利用函数
的应用,及利用函数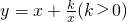 的单调性求函数的最值,属于基础知识的简单综合.
的单调性求函数的最值,属于基础知识的简单综合.
分析:由a>0,b>0利用基本不等式可得,1=a+b
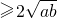 从而可得
从而可得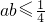 令t=ab则t∈(0,
令t=ab则t∈(0, ]
]通过考查函数
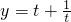 在(0,
在(0,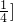 单调性可求函数的最小值
单调性可求函数的最小值解答:∵a>0,b>0
利用基本不等式可得,1=a+b
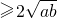 ∴
∴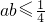
令t=ab则t∈(0,
 ]
]而
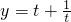 在(0,
在(0,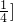 单调递减
单调递减∴当t=
 时函数有最小值
时函数有最小值
故选B
点评:本题主要考查了基本不等式
 的应用,及利用函数
的应用,及利用函数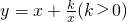 的单调性求函数的最值,属于基础知识的简单综合.
的单调性求函数的最值,属于基础知识的简单综合. 
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
若a>0,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值等于( )
| A、2 | B、3 | C、6 | D、9 |