题目内容
已知抛物线y=ax2+bx+c通过点(1,1),且在点(2,-1)处与直线y=x-3相切,求a、b、c的值.
a=3,b=-11,c=9.
解析:
本题考查导数的几何意义.函数在x=2处的导数等于直线y=x-3的斜率.由题意构造出关于a、b、c的方程组,然后求解.
∵f(1)=1,∴a+b+c=1. ① 2分
又f′(x)=2ax+b,
∵f′(2)=1,∴4a+b=1. ② 5分
又切点(2,-1),∴4a+2b+c=-1. ③ 8分
把①②③联立得方程组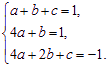 解得
解得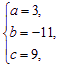 11分
11分
即a=3,b=-11,c=9. 12分

练习册系列答案
相关题目
已知抛物线y=ax2+bx+c与直线y=-bx交于A、B两点,其中a>b>c,a+b+c=0,设线段AB在x轴上的射影为A1B1,则|A1B1|的取值范围是( )
A、(
| ||||
B、(
| ||||
C、(0,
| ||||
D、(2, 2
|