题目内容
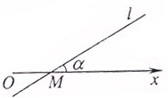 (2012•上海)如图,在极坐标系中,过点M(2,0)的直线l与极轴的夹角a=
(2012•上海)如图,在极坐标系中,过点M(2,0)的直线l与极轴的夹角a=| π |
| 6 |
| 1 | ||
sin(
|
| 1 | ||
sin(
|
分析:取直线l上任意一点P(ρ,θ),连接OP,则OP=ρ,∠POM=θ,在三角形POM中,利用正弦定理建立等式关系,从而求出所求.
解答:解:取直线l上任意一点P(ρ,θ),连接OP,则OP=ρ,∠POM=θ
在三角形POM中,利用正弦定理可知:
=
解得ρ=f(θ)=
故答案为:

在三角形POM中,利用正弦定理可知:
| ρ | ||
sin
|
| 2 | ||
sin(
|
解得ρ=f(θ)=
| 1 | ||
sin(
|
故答案为:
| 1 | ||
sin(
|
点评:本题主要考查了简单曲线的极坐标方程,以及余弦定理的应用,同时考查了分析问题的能力和转化的思想,属于基础题.

练习册系列答案
相关题目
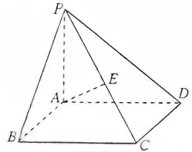 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2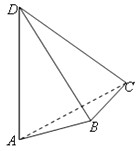 (2012•上海)如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是
(2012•上海)如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是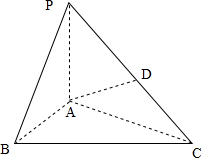 (2012•上海)如图,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点,已知∠BAC=
(2012•上海)如图,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点,已知∠BAC=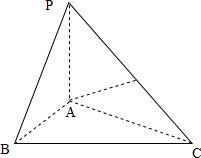
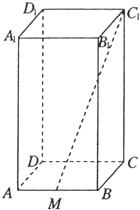 (2012•上海)如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,高为2,M为线段AB的中点.
(2012•上海)如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,高为2,M为线段AB的中点.