题目内容
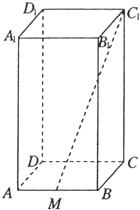 (2012•上海)如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,高为2,M为线段AB的中点.
(2012•上海)如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,高为2,M为线段AB的中点.求:(1)三棱锥C1-MBC的体积;
(2)异面直线CD与MC1所成角的大小(结果用反三角函数值表示).
分析:(1)连接CM,根据M为AB中点,且正方形ABCD边长为1,得到△BCM的面积为S=
S正方形ABCD=
.因为CC1⊥平面ABCD,是三棱锥C1-MBC的高,所以利用锥体体积公式,可得三棱锥C1-MBC的体积;
(2)连接BC1,正方形ABCD中,因为CD∥AB,所以∠C1MB(或其补角)为异面直线CD与MC1所成的角.Rt△MC1B中,可算出BC1=
,而MB=
AB=
,利用直角三角形中三角函数的定义,得到tan∠C1MB=
=2
,所以异面直线CD与MC1所成角为arctan2
.
| 1 |
| 4 |
| 1 |
| 4 |
(2)连接BC1,正方形ABCD中,因为CD∥AB,所以∠C1MB(或其补角)为异面直线CD与MC1所成的角.Rt△MC1B中,可算出BC1=
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| BC1 |
| BM |
| 5 |
| 5 |
解答:解:(1)连接CM,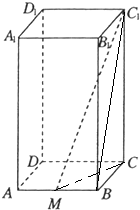
∵正方形ABCD中,M为AB中点,且边长为1,
∴△BCM的面积为S=
S正方形ABCD=
.
又∵CC1⊥平面ABCD,
∴CC1是三棱锥C1-MBC的高,
∴三棱锥C1-MBC的体积为:VC1-MBC=
×
×2=
;
(2)连接BC1
∵CD∥AB,
∴∠C1MB(或其补角)为异面直线CD与MC1所成的角.
∵AB⊥平面B1C1CB,BC1?平面B1C1CB,
∴AB⊥BC1.
Rt△MC1B中,BC1=
=
,MB=
AB=
∴tan∠C1MB=
=2
所以异面直线CD与MC1所成角为arctan2
.

∵正方形ABCD中,M为AB中点,且边长为1,
∴△BCM的面积为S=
| 1 |
| 4 |
| 1 |
| 4 |
又∵CC1⊥平面ABCD,
∴CC1是三棱锥C1-MBC的高,
∴三棱锥C1-MBC的体积为:VC1-MBC=
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 6 |
(2)连接BC1
∵CD∥AB,
∴∠C1MB(或其补角)为异面直线CD与MC1所成的角.
∵AB⊥平面B1C1CB,BC1?平面B1C1CB,
∴AB⊥BC1.
Rt△MC1B中,BC1=
| BC2+CC12 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
∴tan∠C1MB=
| BC1 |
| BM |
| 5 |
所以异面直线CD与MC1所成角为arctan2
| 5 |
点评:本题给出一个特殊的正三棱柱,求其中的异面直线所成角和三棱锥体积,着重考查了棱锥的体积公式和异面直线及其所成的角等知识点,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
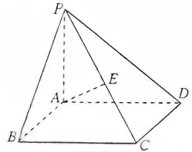 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2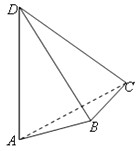 (2012•上海)如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是
(2012•上海)如图,AD与BC是四面体ABCD中互相垂直的棱,BC=2,若AD=2c,且AB+BD=AC+CD=2a,其中a、c为常数,则四面体ABCD的体积的最大值是 (2012•上海)如图,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点,已知∠BAC=
(2012•上海)如图,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点,已知∠BAC=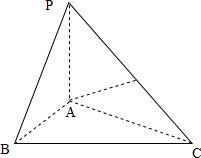
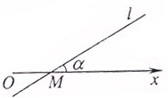 (2012•上海)如图,在极坐标系中,过点M(2,0)的直线l与极轴的夹角a=
(2012•上海)如图,在极坐标系中,过点M(2,0)的直线l与极轴的夹角a=