题目内容
已知关于x的实系数一元二次方程ax2+bx+c=0有两个虚根x1,x2,且(1-3ai)i=c-| a | i |
分析:化简(1-3ai)i=c-
,利用复数相等,求出a,c,代入一元二次方程ax2+bx+c=0,求出两个虚根x1,x2,代入|x1-x2|=1,求出b的值.
| a |
| i |
解答:解:由题设(1-3ai)i=c-
,即:-(1-3ai)=ci-a,得
解得a=1,c=3,
代入方程x2+bx+3=0,求出两虚根为x1=
,x1=
,
于是|x1-x2|=|
-
|=
,
由
=1,得b=
或b=-
.
| a |
| i |
|
代入方程x2+bx+3=0,求出两虚根为x1=
-b+
| ||
| 2 |
-b-
| ||
| 2 |
于是|x1-x2|=|
-b+
| ||
| 2 |
-b-
| ||
| 2 |
| 12-b2 |
由
| 12-b2 |
| 11 |
| 11 |
点评:本题考查复数的基本概念,一元二次方程的根的分布与系数的关系,复数代数形式的乘除运算,复数求模,考查分析问题解决问题的能力,是中档题.

练习册系列答案
相关题目
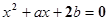 的一根在
的一根在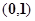 内,另一根在
内,另一根在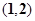 内,则点
内,则点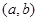 所在区域的面积为
所在区域的面积为 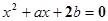 的一根在
的一根在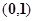 内,另一根在
内,另一根在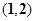 内,则点
内,则点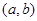 所在区域的面积为
所在区域的面积为