题目内容
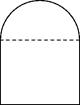
某通讯公司需要在三角形地带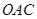 区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域
区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域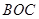 内,乙中转站建在区域
内,乙中转站建在区域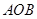 内.分界线
内.分界线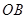 固定,且
固定,且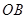 =
=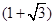 百米,边界线
百米,边界线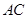 始终过点
始终过点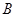 ,边界线
,边界线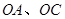 满足
满足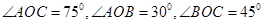 .
.
设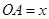 (
(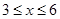 )百米,
)百米,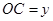 百米.
百米.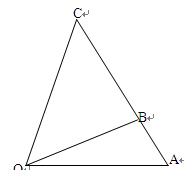
(1)试将 表示成
表示成 的函数,并求出函数
的函数,并求出函数 的解析式;
的解析式;
(2)当 取何值时?整个中转站的占地面积
取何值时?整个中转站的占地面积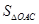 最小,并求出其面积的最小值.
最小,并求出其面积的最小值.
(1)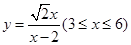 ;(2):当
;(2):当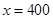 米时,整个中转站的占地面积
米时,整个中转站的占地面积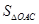 最小,最小面积是
最小,最小面积是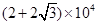 平方米.
平方米.
解析试题分析:(1)要求函数关系式,实际上是建立起 之间的等量关系,分析图形及已知条件,我们可借助于三角形有面积,
之间的等量关系,分析图形及已知条件,我们可借助于三角形有面积,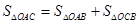 ,从这个等式中,解出
,从这个等式中,解出 ,即得要求的函数式;(2)有了(1)中的关系式,
,即得要求的函数式;(2)有了(1)中的关系式, 就可表示为一个字母
就可表示为一个字母 的式子
的式子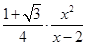 ,它是一个分式函数,由于分母是一次,而分子是二次的,故可这样变形
,它是一个分式函数,由于分母是一次,而分子是二次的,故可这样变形 ,正好这个表达式可以用基本不等式来求得最小值.
,正好这个表达式可以用基本不等式来求得最小值.
试题解析:(1)结合图形可知,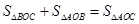 .
.
于是,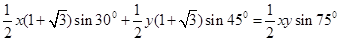 ,
,
解得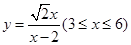 .
.
(2)由(1)知,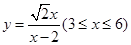 ,
,
因此,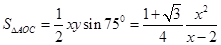

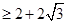 (当且仅当
(当且仅当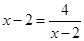 ,即
,即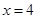 时,等号成立).
时,等号成立).
答:当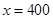 米时,整个中转站的占地面积
米时,整个中转站的占地面积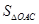 最小,最小面积是
最小,最小面积是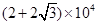 平方米.12分
平方米.12分
考点:求函数解析式,三角形的面积公式,分式函数的最值与基本不等式.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
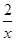 且f(4)=
且f(4)=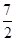 .
.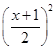 .
.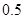 万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.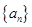 ,每年发放的电动型汽车牌照数为构成数列
,每年发放的电动型汽车牌照数为构成数列 ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;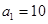
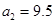
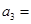
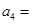
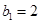

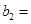 3
3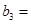
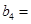
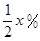 ,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
,该产品每吨的价格上涨百分之几,可使销售的总金额最大?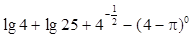 .
. 米,钢筋网的总长度为
米,钢筋网的总长度为 米.
米.