题目内容
(08年沈阳二中四模文)已知点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() ,
,![]()
![]() 。
。
(Ⅰ)当点![]() 在
在![]() 轴上移动时,求点
轴上移动时,求点![]() 的轨迹
的轨迹![]() ;
;
(Ⅱ)过定点![]() 作直线
作直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,试问在
两点,试问在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 成立;
成立;

解析:(Ⅰ)设![]()
![]()
![]()
![]() 且
且![]()
![]()
![]() …………………………………5分
…………………………………5分
∴动点M的轨迹C是以O(0,0)为顶点,
以(1,0)为焦点的抛物线(除去原点)……………………………7分
(Ⅱ)假设存在满足条件的点![]() ,坐标为
,坐标为![]() 。
。
依题意,设直线![]() 的方程为
的方程为![]() ,
,![]() ,则A,B两点的坐标满足方程组
,则A,B两点的坐标满足方程组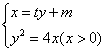 消去
消去![]() 并整理,得
并整理,得![]()
![]() ……………………………………………………………9分
……………………………………………………………9分
设直线AE和BE的斜率分别为![]() ,则
,则
![]() =
=![]()
![]()

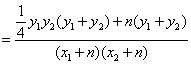
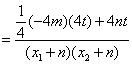
令![]() ................................12分
................................12分
![]()
![]()
![]() ,
,![]()
![]()
所以存在点![]() ,坐标为
,坐标为![]() ,使得
,使得![]() ............14分
............14分

练习册系列答案
相关题目

