题目内容
已知函数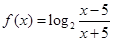
(Ⅰ)求函数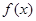 的定义域;
的定义域;
(Ⅱ)若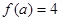 ,求
,求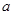 的值;
的值;
(Ⅲ)判断并证明该函数的单调性.
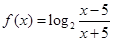
(Ⅰ)求函数
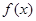 的定义域;
的定义域;(Ⅱ)若
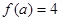 ,求
,求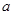 的值;
的值;(Ⅲ)判断并证明该函数的单调性.
(Ⅰ)由 解得
解得 .
.
所以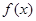 的定义域为
的定义域为 --------------3分
--------------3分
(Ⅱ) -------------------6分
-------------------6分
(Ⅲ)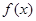 在
在 和
和 上是单调递增的. ---------------7分
上是单调递增的. ---------------7分
证明:任取 ,则
,则 ,
,

 为奇函数 ---10分
为奇函数 ---10分
任取 ,且
,且 ,则
,则 ,
,

 ,
,
 ,
,

由此证得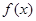 在
在 上是单调递增的. -------12分
上是单调递增的. -------12分
 是奇函数
是奇函数 在
在 上也是单调递增的.
上也是单调递增的.
 在
在 和
和 上是单调递增的.
上是单调递增的.
 解得
解得 .
.所以
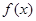 的定义域为
的定义域为 --------------3分
--------------3分(Ⅱ)
 -------------------6分
-------------------6分(Ⅲ)
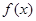 在
在 和
和 上是单调递增的. ---------------7分
上是单调递增的. ---------------7分证明:任取
 ,则
,则 ,
,
 为奇函数 ---10分
为奇函数 ---10分任取
 ,且
,且 ,则
,则 ,
,
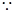
 ,
,
 ,
,

由此证得
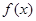 在
在 上是单调递增的. -------12分
上是单调递增的. -------12分 是奇函数
是奇函数 在
在 上也是单调递增的.
上也是单调递增的. 在
在 和
和 上是单调递增的.
上是单调递增的. 略

练习册系列答案
相关题目
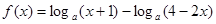 ,(
,(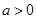 ,且
,且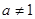 ).
).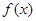 的定义域;
的定义域;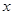 的取值范围.
的取值范围.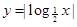 的定义域为
的定义域为 ,值域为
,值域为 ,则
,则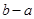 的最小值是
的最小值是 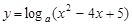 ,当定义域为
,当定义域为 ,值域为
,值域为 ,则
,则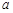 的值为 ▲ .
的值为 ▲ .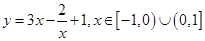 ,则y的取值范围是( )
,则y的取值范围是( )



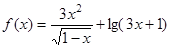 的定义域是 ( )
的定义域是 ( )



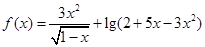 的定义域是( )
的定义域是( )



 的定义域为
的定义域为 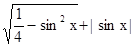 的值域是( )
的值域是( )


