题目内容
函数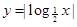 的定义域为
的定义域为 ,值域为
,值域为 ,则
,则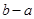 的最小值是
的最小值是
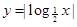 的定义域为
的定义域为 ,值域为
,值域为 ,则
,则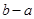 的最小值是
的最小值是 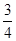
依题意可得, 。当
。当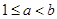 时,则
时,则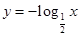 ,此时函数在定义域上单调递增,所以有
,此时函数在定义域上单调递增,所以有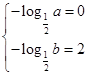 ,解得
,解得 ,此时
,此时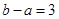 。当
。当 时,则
时,则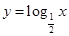 ,此时函数在定义域上单调递减,所以有
,此时函数在定义域上单调递减,所以有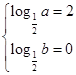 ,解得
,解得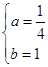 ,此时
,此时 。当
。当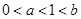 时,
时,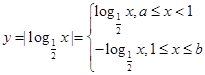 =,,则此时函数在区间
=,,则此时函数在区间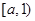 上单调递减在区间
上单调递减在区间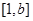 上单调递增。所以函数在
上单调递增。所以函数在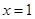 处取到最小值0. 若
处取到最小值0. 若 ,则
,则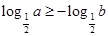 ,此时函数的最大值为
,此时函数的最大值为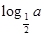 ,从而有
,从而有 ,解得
,解得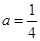 。此时
。此时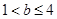 ,所以
,所以 。若
。若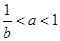 ,则
,则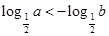 ,则此时函数的最大值为
,则此时函数的最大值为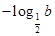 ,从而有
,从而有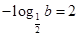 ,解得
,解得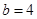 。此时
。此时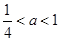 ,所以
,所以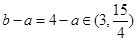 。综上可得,
。综上可得, ,则其最小值为
,则其最小值为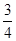
 。当
。当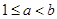 时,则
时,则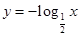 ,此时函数在定义域上单调递增,所以有
,此时函数在定义域上单调递增,所以有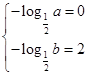 ,解得
,解得 ,此时
,此时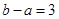 。当
。当 时,则
时,则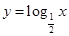 ,此时函数在定义域上单调递减,所以有
,此时函数在定义域上单调递减,所以有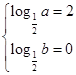 ,解得
,解得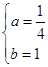 ,此时
,此时 。当
。当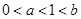 时,
时,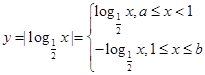 =,,则此时函数在区间
=,,则此时函数在区间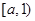 上单调递减在区间
上单调递减在区间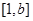 上单调递增。所以函数在
上单调递增。所以函数在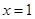 处取到最小值0. 若
处取到最小值0. 若 ,则
,则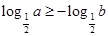 ,此时函数的最大值为
,此时函数的最大值为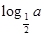 ,从而有
,从而有 ,解得
,解得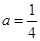 。此时
。此时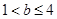 ,所以
,所以 。若
。若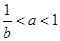 ,则
,则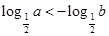 ,则此时函数的最大值为
,则此时函数的最大值为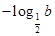 ,从而有
,从而有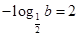 ,解得
,解得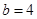 。此时
。此时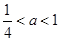 ,所以
,所以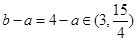 。综上可得,
。综上可得, ,则其最小值为
,则其最小值为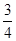

练习册系列答案
相关题目
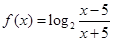
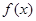 的定义域;
的定义域;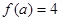 ,求
,求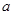 的值;
的值;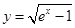 的定义域是( )
的定义域是( )
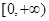


 的值域是 ( )
的值域是 ( )


 的值域为 .
的值域为 . 的定义域是 ( )
的定义域是 ( ) 其中
其中 ,则函数
,则函数 的值域为
的值域为


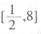
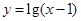 的定义域是:
的定义域是: 的定义域是 ( )
的定义域是 ( ) ∪
∪

 ∪
∪