题目内容
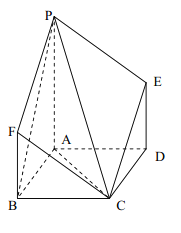
【题目】如图所示,正三角形![]() 所在平面与梯形
所在平面与梯形![]() 所在平面垂直,
所在平面垂直, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 的中点.
的中点.
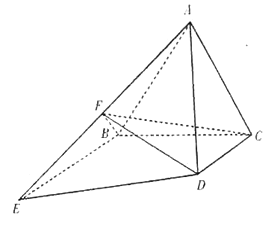
(1)求证: ![]() 平面
平面![]() ;
;
(2)求证: ![]() 平面
平面![]() ;
;
(3)若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)见解析(3)![]()
【解析】【试题分析】(1)运用线面平行的判定定理进行推证;(2)依据题设运用线面垂直的判定定理进行推证;(3)先建立空间直角坐标系,再运用向量的数量积工具进行求解:
(1)如图,取![]() 中点
中点![]() ,连接
,连接![]() ,因为
,因为![]() 为
为![]() 中点,所以
中点,所以![]() 且
且![]() ,
, ![]() ,所以
,所以![]() 且
且![]() ,所以四边形
,所以四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)又因为![]() 为正三角形,所以
为正三角形,所以![]() ,
,
又因为面![]() 面
面![]() ,面
,面![]() 面
面![]() .
. ![]() 面
面![]() ,
,
所以![]() 面
面![]() ,
, ![]() .又因为
.又因为![]() ,所以
,所以![]() 面
面![]() ,所以
,所以![]() 面
面![]() .
.
(3)
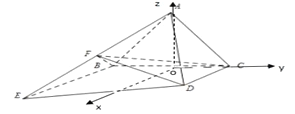
取![]() 中点
中点![]() ,再连接
,再连接![]() .易证
.易证![]() 面
面![]() ,所以
,所以![]() 为直线
为直线![]() 与平面
与平面![]() 所成的角,即
所成的角,即![]() ,设
,设![]() ,可求得
,可求得![]() .
.
以![]() 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系![]() ,则
,则![]() ,
, ![]() ,
, 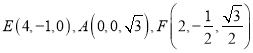 ,
,
所以 ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则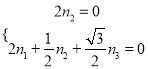 ,令
,令![]() ,得
,得
![]() ,所以
,所以![]() ,
,
设面![]() 的法向量为
的法向量为![]() ,则
,则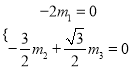 ,令
,令![]() ,得
,得![]() ,
, ![]() ,
,
所以![]() ,所以
,所以 ,
,
因为二面角![]() 为钝角,其余弦值为
为钝角,其余弦值为![]() .
.

练习册系列答案
相关题目
【题目】下表是某校高三一次月考5个班级的数学、物理的平均成绩:
班级 | 1 | 2 | 3 | 4 | 5 |
数学( | 111 | 113 | 119 | 125 | 127 |
物理( | 92 | 93 | 96 | 99 | 100 |
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量![]() ,
, ![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)从以上5个班级中任选两个参加某项活动,设选出的两个班级中数学平均分在115分以上的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:  ,
, ![]()