题目内容
(本小题满分12分)
设函数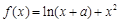 .
.
(Ⅰ)若当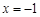 时
时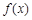 取得极值,求a的值,并讨论
取得极值,求a的值,并讨论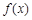 的单调性;
的单调性;
(Ⅱ)若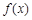 存在极值,求a的取值范围,并证明所有极值之和大于
存在极值,求a的取值范围,并证明所有极值之和大于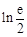 .
.
请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分。做答时请写清题号。
【答案】
(Ⅰ)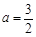 ,当
,当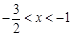 时,
时,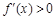 ;当
;当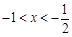 时,
时,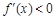 ;当
;当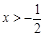 时,
时,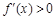 . 从而,
. 从而,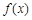 分别在区间
分别在区间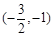 ,
,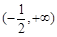 单调增加,在区间
单调增加,在区间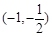 单调减少.
单调减少.
(Ⅱ)若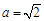 ,
,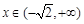 ,
,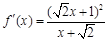 .当
.当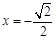 时,
时,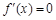 ,当
,当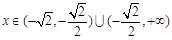 时,
时,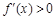 ,所以
,所以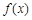 无极值.
无极值.
若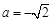 ,
, ,
,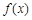 也无极值
也无极值
【解析】解:
(Ⅰ)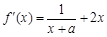 ,
,
依题意有 ,故
,故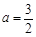 , ……2分
, ……2分
从而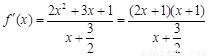 .
.
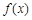 的定义域为
的定义域为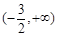 . 当
. 当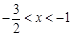 时,
时,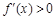 ;当
;当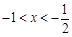 时,
时,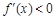 ;当
;当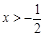 时,
时,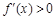 . 从而,
. 从而,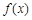 分别在区间
分别在区间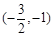 ,
,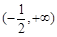 单调增加,在区间
单调增加,在区间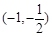 单调减少.
……5分
单调减少.
……5分
(Ⅱ)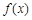 的定义域为
的定义域为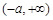 ,
,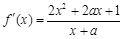 .
.
方程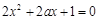 的判别式
的判别式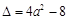 .
.
(ⅰ)若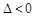 ,即
,即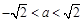 ,在
,在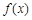 的定义域内
的定义域内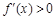 ,故
,故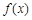 无极值.
无极值.
(ⅱ)若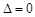 ,则
,则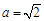 或
或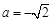 .
.
若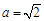 ,
,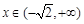 ,
,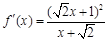 .当
.当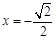 时,
时,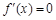 ,当
,当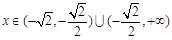 时,
时,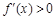 ,所以
,所以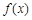 无极值.
无极值.
若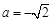 ,
, ,
,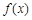 也无极值. ……7分
也无极值. ……7分
(ⅲ)若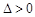 ,即
,即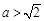 或
或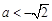 ,则
,则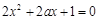 有两个不同的实根
有两个不同的实根
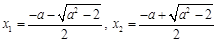 .
.
当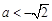 时,
时,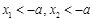 . 从而
. 从而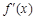 在
在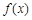 的定义域内没有零点,故
的定义域内没有零点,故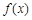 无极值.
无极值.
当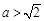 时,
时, ,
,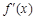 在
在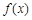 的定义域内有两个不同的零点,由极值判别方法知
的定义域内有两个不同的零点,由极值判别方法知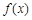 在
在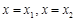 取得极值.
取得极值.
综上,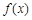 存在极值时,a的取值范围为
存在极值时,a的取值范围为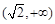 .
……10分
.
……10分
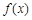 的极值之和为
的极值之和为
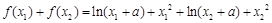
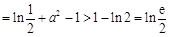 .
……12分
.
……12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目