题目内容
设不等式组
|
(1)求f(1)、f(2)的值及f(n)的表达式;
(2)设bn=2nf(n),Sn为{bn}的前n项和,求Sn;
(3)记Tn=
| f(n)f(n+1) |
| 2n |
分析:(1)据可行域,求出当x=1,x=2时,可行域中的整数点,分别求出f(1),f(2),f(n).
(2)由于数列的通项是一个等差数列与一个等比数列的积构成的新数列,利用错位相减的方法求出数列的和.
(3)求出
,据它的符号判断出Tn的单调性,求出Tn的最大值,令m大于等于最大值即可.
(2)由于数列的通项是一个等差数列与一个等比数列的积构成的新数列,利用错位相减的方法求出数列的和.
(3)求出
| Tn+1 |
| Tn |
解答:解:画出
的可行域
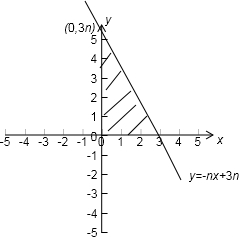
(1)f(1)=2+1=3
f(2)=3+2+1=6
当x=1时,y=2n,可取格点2n个;当x=2时,y=n,可取格点n个
∴f(n)=3n
(2)由题意知:bn=3n•2n
Sn=3•21+6•22+9•23+…+3(n-1)•2n-1+3n•2n
∴2Sn=3•22+6•23+…+3(n-1)•2n+3n•2n+1
∴-Sn=3•21+3•22+3•23+…3•2n-3n•2n+1
=3(2+22+…+2n)-3n•2n+1
=3•
-3n2n+1
=3(2n+1-2)-3nn+1
∴-Sn=(3-3n)2n+1-6
Sn=6+(3n-3)2n+1
(3)Tn=
=
∴T1<T2=T3>T4>…>Tn
故Tn的最大值是T2=T3=
∴m≥
.
|

(1)f(1)=2+1=3
f(2)=3+2+1=6
当x=1时,y=2n,可取格点2n个;当x=2时,y=n,可取格点n个
∴f(n)=3n
(2)由题意知:bn=3n•2n
Sn=3•21+6•22+9•23+…+3(n-1)•2n-1+3n•2n
∴2Sn=3•22+6•23+…+3(n-1)•2n+3n•2n+1
∴-Sn=3•21+3•22+3•23+…3•2n-3n•2n+1
=3(2+22+…+2n)-3n•2n+1
=3•
| 2-2n+1 |
| 1-2 |
=3(2n+1-2)-3nn+1
∴-Sn=(3-3n)2n+1-6
Sn=6+(3n-3)2n+1
(3)Tn=
| f(n)f(n+1) |
| 2n |
| 3n(3n+3) |
| 2n |
|
∴T1<T2=T3>T4>…>Tn
故Tn的最大值是T2=T3=
| 27 |
| 2 |
∴m≥
| 27 |
| 2 |
点评:求数列的前n项和,先求出数列的通项,据数列通项的特点,选择合适的求和方法;解决数列的单调性问题只能通过判断相邻项的差的符号或相邻项的比与1的大小.

练习册系列答案
相关题目
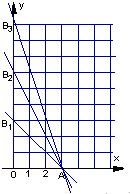 在平面直角坐标系上,设不等式组
在平面直角坐标系上,设不等式组